Physics-Informedニューラルネットワーク wi2 ニューラル演算子
日本では、2020年6月30日に宇宙基本計画ver.1が閣議決定された(ver.2は、2023年6月13日閣議決定)。20年5月には、日本の宇宙利用の優位を確保するため、航空自衛隊府中基地に「宇宙作戦隊」が新編された。宇宙領域把握(SDA)に関する取組(防衛省、2023年11月28日)†1では、「宇宙作戦能力を強化するため、SDA体制の整備を確実に推進することが重要である」と強調されている。経団連も、「宇宙の安定的な利用を確保するためには、デブリや不審な衛星の動向など宇宙の状況を把握する必要がある」として、「SDA衛星の2026年度打上を達成すべきである」と主張している†2(もっとも、防衛省の意向を汲んでいるだけだろう)。
米MITリンカーン研究所†3は、「人工衛星に作用する”モデル化されていない加速度”をPINNsで学習することで、衛星軌道を正確に予測できた」と主張する論文(以下、本論文[*85])を公開した(24年3月28日@arXiv)。 ☛モデル化されていない加速度は、後述。
†1 https://www8.cao.go.jp/space/comittee/27-anpo/anpo-dai58/siryou2.pdf
同資料において、以下のように用語定義が行われている。SDAは、SSAに加えて「宇宙機の運用・利用状況及びその意図や能力を把握すること」。SSAは宇宙状況把握(Space Situational Awareness)の略語であり、「宇宙物体の位置や軌道等を把握すること(宇宙環境の把握を含む)」。
†2 https://www.keidanren.or.jp/policy/2024/017_honbun.html
†3 米連邦政府機関御用達大学であるMITにおける、航空防衛(攻撃に使用される研究はしないらしい)に特化した研究所。国防総省が設立した研究所の運営をMITが受託しているという、米国でよくある形態。古い資料(https://repository.dl.itc.u-tokyo.ac.jp/record/21065/files/sk029007015.pdf)によれば、年間予算の約90%が国防総省との契約に基づく収入である。
【1】本論文の主張
「逆問題、外挿」というPINNsにとって得意なワードが含まれている。
(1) PINNsによって、「対地同期軌道†4(GEO)上の人工衛星に作用する、”モデル化されていない加速度”を、学習することができた」。これは、衛星軌道調整(フィッティング)の文脈で、逆問題を解いたことを意味する。 ☛モデル化されていない加速度は、後述。
(2) PINNsは、20日後の衛星軌道を高精度に予測できた。これは、外挿が、高精度に行えたことを意味する。
†4 赤道上の対地同期軌道は、静止軌道と呼ばれる。
【2】事前整理
(1) モデル化されていない加速度
軌道状態†5を、物体と相関する観測値に適合させることによって、衛星軌道は維持される。観測値は、宇宙監視専用の光学センサーとレーダー センサーで構成される宇宙監視ネットワークによって得られる。米国では、衛星軌道の維持は、米国防総省の一部である、第18宇宙防衛飛行隊によって行われている(らしい)。
過去数十年にわたり、衛星が軌道を変更するためにスラスターを積極的に使用していないことを前提として、衛星が「いつ・どこに存在しているか?」を、迅速かつ正確に予測するために使用できる、高忠実度の物理モデルが開発されてきた。それらの高忠実度物理モデルは、地球重力、大気抗力(大気ドラッグ)、太陽輻射圧(SRP)効果、太陽・月・その他の天体からの重力摂動なども考慮する、高品質な物理モデルである。たとえば、2行軌道要素形式(Two Line Element set:TLE)†6から衛星の位置と速度を予測するために使用される Special General Perturbations 4(SGP4)プロパゲータは、地球の重力、大気抵抗、太陽と月による摂動を考慮している。しかし、衛星の推力は考慮されていない。この衛星推力は、モデル化されていない加速度の発生源の一つである。
常駐宇宙物体(Resident Space Object:RSO)†7の中には、モデル化されていない加速度を考慮しなければ、軌道予測が困難なRSOが存在する。例えば、㊀軌道を変更するために、低推力の電気推進(☛下記(1)を参照)を使用する衛星や、㊁既存のモデルで考慮されている以上の SRP 効果を受ける非常に高い面積質量比(HAMR)を持つデブリ、があげられる。
†5 2行軌道要素形式(TLE)または、位置および速度ベクトルのいずれか。TLEは、下記†6を参照。
†6 TLEとは、北米航空宇宙防衛司令部が、監視し公開している人工衛星を含む宇宙物体の軌道情報
を2行形式で表したもの
(出所https://gportal.jaxa.jp/gpr/assets/mng_upload/GCOM-W/TLE.pdf)。
†7 RSOには、活動中・非活動中の宇宙船、ロケット本体や(ロケットの)上段、制御不能なスペースデブリなどが含まれる
(出所https://crds.jst.go.jp/dw/20240402/2024040237805/)。
(2) 軌道予測が困難な理由
前項で、 モデル化されていない加速度を考慮しなければ、軌道予測が困難なRSOも存在することを述べた。その理由を整理しよう。以下では、分かり易さを優先して、RSOを人工衛星に限定する。今日、衛星の大部分は、何らかの推力を使用して正確な軌道を維持している。特に、電気推進(イオン推進、ホール効果スラスター、パルスプラズマスラスターなど)は燃料効率が向上するため、よく利用されている。
電気推進システムと化学スラスタの重要な違いの 1 つは、化学スラスタは数秒で大きな加速を達成できるのに対し、電気推進システムは数分から数日間継続的に低推力を適用すること、である。化学スラスターを使用して短期間に大きな加速を加える衛星の場合、軌道状態の変化が瞬間的に起こる。このため、センサーにタスクを割り当て、衛星の新しい観測値を関連付け、操縦後の新しい状態を推定する機会が与えられる。端的に述べると、未知のノイズが混入するするものの、短期間であるため、衛星のダイナミクスによる影響は軽微(従前のダイナミクスは、失われていない)と表現できるだろう。
一方、低推力を数日間継続的に適用する電気推進システムを使用する衛星(以下、「推進衛星」と呼称)は、軌道移動操作終了時の衛星位置は、操作開始時の位置から、非常に遠く離れている可能性がある。そのため、新しい観測値を、衛星の以前の軌道状態と明確に関連付けることは困難である。これも端的に述べると、長期間に渡って未知のノイズが混入したため、従前のダイナミクスに関する知識はもはや失われた、と表現できるだろう。従って、新たにダイナミクスを構築する必要がある(しかも、電気推進システムを使用する度に、継続的に)。
推進衛星の軌道状態は、実態として、試行錯誤的な手動介入によって維持されている。この手動介入は、絶えず変化する軌道状態に対応するために、頻繁に繰り返す必要がある(ので時間とコストを要する)。また、手動介入による維持では、例えば光学センサー・サイトの気象停止等により、新しい観測値がすぐに受信されない場合、推進衛星が完全に失われる可能性がある。
【3】本論文のアイデア
(1) モデルの学習
1⃣ モデルの構築指針
推進衛星における軌道変更後のダイナミクスを構築するには、衛星に作用する自然力と人工推力の両方を含む、衛星の総加速度を計算するモデルを構築する必要がある。本論文は、このモデルを「物理モデルと深層学習モデルの組み合わせ」により構築する。具体的には、Physics-Informedニューラルネットワーク(PINNs)を適用する。当該軌道予測の問題形式が逆問題であり、さらに外挿の成功が有用であるため、PINNsが選択されたと考えられる。
簡単にまとめると、PINNsにおいてモデル化する物理量は、推進衛星に働く「加速度」である。モデル出力は、推進衛星の(衛星軌道上の)位置及び速度である(速度については、分かり易さを優先して、本稿では触れていない)。位置=∫(∫加速度dt)dtなので、モデル・アーキテクチャ的には、ニューラルODEと見做すことができる。
2⃣ 損失関数
総損失関数は、「物理モデルからの損失関数+人工推力に対応する深層学習モデルからの損失関数」、である。総損失関数は、モデル・パラメーターに関する勾配を決定するために、ODEソルバー†8を通じて逆伝播される。
総損失関数の前者は、いわゆるPDE損失である。後者は、 逆問題の損失関数である。逆問題の損失関数は、観測残差(=実測観測値ー予測観測地)の平均二乗誤差(MSE)で計算される。衛星の位置ベクトルと速度ベクトルは、軌道伝播†9によって決定される。(軌道伝播によって決定された)位置ベクトルと速度ベクトル⊕センサーの位置と速度、から予測観測値を導出できる。
†8 (常)微分方程式ソルバー
†9 ある時刻にある位置・速度で運動をしている人工衛星が、その後の時刻において、どの位置・速度にいるのかを計算すること。
3⃣ 初期条件の調整
モデル学習プロセスの一部として、ネットワーク・パラメーターに加えて、衛星の初期位置と速度ベクトルも調整される。これは、㈠モデル内に調整可能なパラメーターとして初期条件を含めるか、㈡これらのパラメーターをモデルから除外して個別に解決する、ことによって実現できる。本論文では、両者が評価され、㈡がより優れていると判明した。
具体的には、初期条件は、学習ループの N 回の反復ごとに 1 回、観測データに適合する単純なバッチ最小二乗法を使用して推定される。100学習ステップごとに、初期条件をフィッティングすると、良好なパフォーマンスが得られることがわかった。
(2) ニューラルネットワークのハイパーパラメータ等
アーキテクチャ・・・多層パーセプトロン
隠れ層数・・・2
活性化関数・・・tanh(双曲線正接関数)
オプティマイザ・・・Adam
エポック数・・・2万
学習率初期値・・・3×10-3
学習率スケジューリングのステップサイズ・・・100
学習率スケジューリングのスケールファクター・・・0.98
(3) データセット
地上のパッシブ光学望遠鏡から観測された、GEO上にある推進衛星の角度のみを、入力データとする。データは 2 日間にわたり、赤経と赤緯†10において30 回測定され、時間内にランダムにサンプリングされた。 測定誤差は、平均値ゼロ、標準偏差0.5秒角のガウス分布を、ランダム・サンプリングすることにより観測値に追加された。
†10 赤経(right-ascension:RA)は、春分時の太陽の位置を0時とし、地球の自転の方向に24時まで定めた方位。赤緯(declination:Dec)は、天の赤道を 0°とし、北極方向を正として±90°まで定めた角度。
【4】比較結果
(1) 比較対象と比較指標
❶PINNsと比較されるモデルは、❷物理モデル単体である。本論文のPINNsは、物理モデルと深層学習モデルを組み合わせモデルであった。比較指標は、二乗平均平方根誤差(RMSE)である。
(2) 観測誤差と外挿誤差
1⃣ 観測誤差
PINNのRMSEは 1.00秒角。一方、物理モデル単体のRSMEは、123 秒角であり、2 桁改善された。
2⃣ 外挿誤差
モデルが、衛星軌道をどの程度正確に予測できるかを評価した。学習期間終了から1日後、5日後、20 日間後の、予測伝播位置と真の伝播位置との差(km)を算出し、比較した(20 日間後は図からの目分量)。結果は、1日後❶3.35km❷397km、5日後❶164km❷3,860km、20日後❶およそ1万5,000km❷およそ3万5,000km、である。1日後は2桁の改善、5日後は1桁の改善、20日後は2倍程度の改善である。静止軌道を3万6千kmとすると、静止軌道の周長は226万km程度だから、周長の1/10程度ズレている計算になる。
【5】感想
(1) PINNsに限らず、どのようなツール・アルゴリズム・アーキテクチャ・方法論でも、唯一無二の絶対王者は存在しない。必ず、得手不得手がある。機械学習・深層学習に限定すれば、唯一無二は存在しないことが証明されている(らしい)。PINNsも、非線形性問題に弱いと指摘され、意外と有効範囲が狭いという評価を受けているように思える。しかし実務家として重要なことは、手持ちのツールが有効な領域を特定し、そこで違いを出すということであろう。その意味で、本論文は、面白いところにPINNsを適用したと感じる。
(2) 本論文の学習データ(入力データ)は、角度のみである。地上のパッシブ光学望遠鏡で正確に観測できる値だけを使用している。レーダーセンサーを使うと、距離と測度の情報も取得できる。普通に考えて、入力データをリッチにすると、出力(結果)もリッチになると思われる。そこは、敢えて公開していないのだろうか。
ニューラルネットワーク(NN)を使った代理モデルは、その洗練さ、柔軟性の高さ、観測データの組み込みの容易さにより、従来の数値ソルバーに代わる魅力的な選択肢と期待されている。PINNsはNNを使った代理モデルの代表と考えられているものの、誤った解に収束することも多く、その学習は難しいことが知られている。このPINNsにおける学習の困難を、本稿ではシンプルに、学習障害と呼称する。
ニューラルネットワークによる学習モデル(深層学習モデル)の性能は、極端に言えば、全てデータにかかっている。この教義をPINNsにあてはめると、PINNsの性能は、損失(関数)に関する最適化計算に用いるデータが全て、ということになる。ここで、学習障害対策の先行研究を概観すると、[*40]では、以下の3つを上げている:㊀時間的因果関係の尊重(【2】(2)2⃣参照)、㊁PINNsの損失関数(PDE†0損失、初期損失、境界損失)にかかる重みを、適応的に調整する、㊂カリキュラム学習。また、[*74]では、PINNsの課題に対する対策(の一つ)として、損失関数にかかる重みの変更及び、再サンプリングを上げている。
教義にあてはめるとデータが全て、である。コロケーション点が十分にあればPINNsの性能は高くなるが、同時に計算コストも高くなる。PINNsを代理モデルとして用いる場合、数値ソルバーより計算が遅ければ意味がない(場合により、PINNsが有限要素法より遅い、という論文はこちら)。そこで、コロケーション点の数に関して、良い塩梅を探す意味が出てくる。
PINNsに文脈におけるコロケーション点とは、数値が紐付いた点を意味する。ここで言う数値とは、入力値並びに出力値である。先行研究を見ると、間接的にコロケーション点を調整していることがわかる(※)。損失にかかる重みを調整して、間接的×間接的にコロケーション点を調整するか、サンプリングで間接的にコロケーション点を調整している。本稿では、コロケーション点の構成を扱った論文を2つ取り上げている。一つ目の[*87]は、コロケーション点を直接調整するアプローチを扱っている。二つ目[*88]は、サンプリングで間接的にコロケーション点を調整するアプローチを扱っている。
†0 物理や数理解析の文脈でPDEは、偏微分方程式(Partial Differential Equation)の略であるが、本稿では意図的に混同して、支配方程式そのものに対する略称にもPDEをあてる。
※ 「間接的にコロケーション点を調整している、という統一的な見方が可能」という表現が、正しいかもしれない。間接的の意味が分かり難いが、間接≠直接であり、「書き下せる規則に従って、コロケーション点を(直接)拾い上げる」ことを直接(的)と言っている(つもり)。
【1】論文の主張
(0) 前説
フィンランド・アールト大学[*86]の研究者は、「アルゴリズムを改良して、PINNs学習の安定性を高めた」を主張する論文[*87]を発表した(23年1月11日@arXiv)。学習の安定性については、【7】(1)を参照。結構重要な論文だと思っている。
英リーズ大学及びロンドン大学の研究者による論文[*88](24年4月18日@arXiv)は、幅広いケースで優れた性能を示すサンプリング手法を構築した、とする。
(1) [*87]の主張
「相対L2誤差†1を小さくできる、バニラPINNsに対するアルゴリズムを開発した」と主張する。この場合のアルゴリズムは、損失(関数)に対する最適化計算用コロケーション点を構成するアルゴリズムである。開発したアルゴリズムの有効性を、対流方程式に加えて、反応方程式・反応拡散方程式・拡散方程式に対して、実証した。
†1 為念:相対L2誤差=||真値ー予測値||2/||真値||2。||・||2は、L2ノルム(≒ユークリッド距離)。
(2) [*88]の主張
PDE損失の計算に用いるコロケーション点のサンプリングにおいて、「独立変数に関する残差の混合微分に基づく、コロケーション点位置の確率分布を使った、適応サンプリングは優れている」と主張する。対象とした方程式はバーガース方程式とアレン=カーン方程式であり、多種多様なケースで、固定サンプリング等と比較した。
【2】事前整理
(1) 学習障害の原因と対策
[*87]では、学習障害の原因を、以下のように特定している。まず、PINNsの実際の失敗例から、次の洞察を得た:PINNs が一部の領域(たとえば、初期条件から遠く離れた領域)で、単純†2で局所的に一貫した解を見つけると、それを変更するのは非常に困難になる場合がある。これにより、正しい解と間違った解を組み合わせた、最終的な解が得られてしまう。
その上で、学習障害を次のように整理した:「初期条件から遠く離れた点」が、PINNsのPDE損失に寄与する場合、解を悪い局所最適に向かって引っ張ることによって最適化手順を悪化させる可能性がある。一方、学習開始時点において、PDE損失に「初期条件から遠く離れた点」を含めることには、ほとんど利点がない。
そのように学習障害を理解した上で、対策を考案した:損失関数の最適化計算に用いるコロケーション点を、規準に則って構成する(☛【3】(2)参照)。
†2 空間的な構造を示さない、均一・一様な解を単純と呼んでいるようである。
(2) [*87]における学習障害対策の先行研究整理
1⃣ 時間適応戦略
時間区間を部分区間に分割し、各部分区間で PINNs を順次学習することにより、学習障害に対処するアプローチは、時間適応戦略と呼ばれる。 時間適応戦略により、PINNs の学習手順は、初期条件から時間区間のもう一方の端(終端点)に向かって、徐々に移動する解を計算する、古典的数値ソルバーと同様になる。 少しだけ詳しく述べると、時間区間[T1、T2]が複数の部分区間に分割され、PDEは個別の PINN によって、部分区間ごとに順番に解かれる。前の部分区間の境界にある解が、次の部分区間の初期条件として使用される。
2⃣ 時間的因果関係の尊重
”時間依存”PDE を解くときに PINNs が時間的因果関係に違反する可能性があるため、誤った解に収束しやすいことが示されている。これは、PINNs がすべての PDE残差を同時に最小化する傾向がある一方で、初期の正しい解を取得する前であっても、後の時点で PDE残差を最小化する方向に望ましくない偏りがあるためである。
この問題の対応策は、時間軸に沿った重み「時間的重み」を導入することである。この重みは(時間軸上で)直前のPDE累積損失を使用して計算される。当該対応策の本質は、(時間軸上で)以前のすべての点で、解が適切に近似されるまで、初期条件から遠く離れた点の影響をゼロにすることである。
(3) [*88]によるコロケーション点サンプリング手法の整理
1⃣ 概要
PINNsのオリジナル実装では、固定数のコロケーション点が系全体に、ランダムかつ均一に分散される。ただし、特定の問題では、一部の領域は他の領域よりも本質的に学習が難しく、純粋にランダムなアプローチでは学習が遅くなったり、非効率になったりする可能性がある。異なるコロケーション点には、異なる量の学習情報が含まれる。これは、コロケーション点の分布を調整することが、学習効率の点で有益である可能性を示唆する。また、コロケーション点の分布調整は、学習中にネットワークが極小値に陥るリスクを最小限に抑えることにも繋がる(ので有益である)。
ただし、どの領域が最も重要になるかについての先験的な知識が必要である等の理由により、コロケーション点の分布を、手動で調整するのは困難である。単純な代替案は、コロケーション点の数を増やすことであるが、計算コストが大幅に増加する。実用的な意味での、コロケーション点の最適な分布または良好な分布を見つける手法としては、 2 つの一般的なアプローチがある。
㈠ 固定されたコロケーション点を持つが、それらの重み付けを異なる方法で行う。つまり、適応重み付け、である。領域内における、特定コロケーション点の影響を重み付けして、主要なコロケーション点が見落とされないようにする。
㈡ コロケーション点の位置を調整する。つまり適応(型)再サンプリングである。
2⃣ サンプリングの規準
サンプリングの観点から見ると、既存方法は基本的に、明示的なパラメータ化、または陰的近似のいずれかを介して、コロケーション点の理想的な分布を求める。理想的な分布を求めるために利用されている情報は、コロケーション点における局所PDE残差や、コロケーション点の位置に関する損失関数の導関数など、主に損失関数に焦点を当てている。
これに対して[*88]は、推定解と残差の混合導関数に基づいた代替規準を検討する。
【3】[*87]が開発したアルゴリズム
(1) アルゴリズムの概要とセットアップ
0⃣ 概要
[*87]のPDEは、初期値・境界値問題として解かれる、という設定である(もちろん、これは標準的な設定)。その設定の下、[*87]で提案されている、学習障害を解消するPINNs学習アルゴリズムは、時間軸と空間軸の双方で工夫がなされている。
時間軸では、時間適応戦略を踏襲する。時間適応戦略は、時間区間を分割して、分割した部分区間ごとにPINNs学習を行う。このため結果的に、異なる初期値で学習を行う形式の「アンサンブル学習」となる。空間軸では、損失に関する最適化計算用コロケーション点(以下、単に、コロケーション点)を拾い上げていくする領域を規準に則って、徐々に拡大するというアプローチを採用する。
1⃣ アンサンブル一致度
PINNアンサンブルのメンバーは通常、コロケーション点近傍では同じ解に収束するが、コロケーション点から遠く離れたところでは、異なる間違った解を好む可能性がある。このため、アンサンブルの一致度を、「コロケーション点をPDE損失を計算する点に含める」ための規準として使用することができる。なお、上記「コロケーション点をPDE損失を計算する点に含める」の意味は、アンサンブル一致度によって追加(条件を与える点が追加及び、新しい初期条件が追加)された初期条件を使って、PDE損失計算を行うという意味である。アンサンブル一致度は、アンサンブル学習で出力される予測値(以下、アンサンブル予測値)の分散として計算される†3。
2⃣ セットアップ
初期損失を計算する初期条件データセットをDとする。境界損失計算用コロケーション点候補の集合をB、実際に選択されたコロケーション点の集合をB’とする。同様に、PDE損失に対して、PとP’を設定する。
†3 [*87]で、言葉で明示されているわけではないが、アルゴリズム(5頁のAlgorithm 1 Training PINNs with label propagation)において表現されている。
(2) アルゴリズムの詳細
1⃣ 詳細アルゴリズム壱・PDE損失
アルゴリズムは、以下の通りである:Dの中で、PDE損失に関するソフト制約†4を満たす点の集合を、まず作成する。この集合をD’とする。ソフト制約は、アンサンブル予測値の平均に対して課されている。D’の点とPの点との最短距離が、”しきい値”†5未満の点を抽出して、P’を作成する。つまり、PDE損失は、初期条件を設定した点との距離が近い点から計算が実行される。この「楽な箇所から初めて、困難な箇所に進む」というアプローチは、カリキュラム学習と発想が似ている。
DはPの点を一部加えて、ゆっくり膨張していく(下記3⃣を参照)。膨張したDをD+と表現する。このためP’を構成する点は、Dから見て遠く離れた点を、徐々に加えていく(=PDE損失を計算するコロケーション点が拡大していく)仕組みになっている。なお、コロケーション点の構成は、コロケーション点候補の全てに、当該アルゴリズムが適用されるまで継続される(これは、境界損失、初期損失でも同様)。
2⃣ 詳細アルゴリズム弐・境界損失
PDE損失の場合とアルゴリズムは、同じである:D’の点とBの点との最小距離が、”しきい値”†5(再)未満の点を抽出して、B’を作成する。境界損失も、初期条件を設定した点との距離が近い点から計算が実行される。
3⃣ 詳細アルゴリズム参・初期損失
初期損失の場合のアルゴリズムは、他と大きく異なる:P’の(コロケーション)点を使って求めたアンサンブル予測値に対して、中央値と分散を計算する。次の㈠及び㈡が満たされれば、P’のコロケーション点における、アンサンブル予測値の中央値を「疑似的な初期値†6」とする:㈠分散がしきい値未満†7。㈡P’のコロケーション点とD’の点との最短距離が、しきい値未満†8。P’のコロケーション点と「疑似的な初期値」がDに追加され、D+となる。
†4 ε未満で十分であることを意味する。[*87]では、ε=0.001(デフォルト値)。
†5 具体的には、0.1(デフォルト値)。
†6 [*87]では、「擬似ラベル」と呼ばれている。
†7 この場合のしきい値は、4×10-4(デフォルト値)。
†8 この場合のしきい値は、0.05(デフォルト値)。
(3) 2つのバージョンと損失関数の重み
[*87]では、損失関数の重みを適応的に変化させるというアプローチを採用せず、固定数として扱う。損失関数の重みが固定数の場合、重み=損失関数を計算するために用いるコロケーション点の数、とすることは、普通である。
❶アンサンブル・バージョンの場合、損失関数の重みは、次のように設定される:境界損失の重みwB = 1/|B’|、PDE損失の重みwPDE= 1/|P’| 及び初期損失の重みwS= 1/|D|。ここで、アンサンブル・バージョンとは、PDE損失の計算にのみ、D+を使用するバージョンを指している†9。|B’|は、境界損失を計算するために用いるコロケーション点の数である。|P’|は、PDE損失を計算するために用いるコロケーション点の数である。|D|は、初期失を計算するために用いるコロケーション点の数であり、初期条件を与える点+擬似ラベル点の数である†10。
❷擬似ラベル・バージョンの場合、損失関数の重みは、次のように設定される:境界損失の重みwB = 1/|B’|、PDE損失の重みwPDE= 1/|P’| 及び初期損失の重みwS= 1/|D+|。擬似ラベル・バージョンとは、D+を使用して、PDE損失と初期損失の両方を計算するバージョンを指している。
以降、❶及び❷を『提案手法』と呼称する。
†9 [*87]内でアルゴリズムを説明している箇所(5頁のAlgorithm 1 Training PINNs with label propagation)では、アンサンブル・バージョンは、D+を使わずにDを使うと書かれている(ただし、[*87]の表記は、DがDLで、D+はDL∪DPL)。これは、6頁の記述(2. PINN Ensemble (Ens):)と整合がとれていない。本稿では、6頁の記述を正としている。
†10 擬似ラベル点の数を加えていることは、矛盾するのではないかと思うが、原論文ママ。
(4) まとめ
アンサンブル学習である[*87]のPINNsに対する、工夫された学習アルゴリズムは、規律のとれたコロケーション点の構成とまとめることができるだろう。無計画で野放図に構成するのではなく、初期条件を与える点の近くからPDE損失用のコロケーション点を、徐々に拾い上げていく。こうすることで、悪い影響しかもたらさないコロケーション点を除外している。
(5) ハイパーパラメータ等
Adamの学習率・・・1.0×10-3
隠れ層の数・・・4
隠れ層のニューロン数・・・50
活性化関数・・・tanh(双曲線正接関数)
LBFGS†11適用のタイミング・・・PDE損失に寄与するコロケーション点の更新前と学習の最後。
†11 LBFGSはL-BFGSとも表記される。
【4】[*87]の検証結果
(0) 検証の対象とした物理系(支配方程式)
掲題の物理系は、以下の通りである。なお、コロケーション点の数は、PDE損失が1,000、初期損失が256、境界損失が100である。
① 周期的境界条件を課した、対流方程式
② 周期的境界条件を課した、化学反応のモデル化に使用される反応システム
③ 周期的境界条件を課した、反応拡散方程式
④ 周期的境界条件を課した、拡散方程式
⑤ ディリクレ境界条件を課した、拡散方程式
(1) 提案手法との比較:比較対象モデル及び、比較指標
比較対象としたPINNsは、以下の4種類である:⓵バニラPINN、⓶SA-PINN、⓷時間的因果関係を尊重したバニラPINN(☛【2】(2)2⃣参照)、⓸bc-PINN。以降、⓵~⓸を『既存手法』と呼称する。なお、表記は[*87]に従った。
SA-PINNは、Self Adaptive-PINNの略であり、損失関数の重みを自己適応的に変化させる。本質的には、解の導出(つまりは、パラメータ導出に関する最適化計算に相当する)に重要な領域から、多くサンプリングすることで、学習性能をあげる。
bc-PINNは、backward compatible PINNの略である。bc-PINNの問題意識は、非線形性が強く高次の偏微分方程式に対しては、PINNの精度は著しく低下する、ということである。そして、この問題を解決するために、単一のニューラルネットワークを用いて、連続する時間区間にわたってPDEを逐次的に解くというスキームを提示した。[*87]でいうところの、時間適応戦略を採用した、アンサンブル学習である。bc-PINNは、サンプリングに工夫を凝らしておらず、時間区間の分割及びサンプリングが固定的である。
[*87]では具体的には、時間区間は4分割され、PDE損失を計算するために各区間で 250 個のコロケーション点を構成し、境界損失を計算するためには25 個のコロケーション点を構成している。
比較指標である相対L2誤差は、異なるランダム・シードを使用した10回の学習過程にわたる平均値として算出した。
(2) 記述手法と提案手法との比較結果
0⃣ 比較に関する詳細
既存手法は既述済だが、オプティマイザを含めて、詳細に記述する。
基本的に、 オプティマイザは、㊀Adam、㊁LBFGS、㊂Adam+LBFGS、が使用された。ただし、⓷はAdamのみ(と思われる)。また、⓶のオプティマイザは、①~③においてはAdamのみであるが、④と⑤では、Adam及びAdam+LBFGSが使用されている。提案手法では、㊀と㊂が用いられ、㊁は用いられていない。
既存手法は、①~③では、物理パラメータを2パターン考慮するので、それぞれ14種類存在する: (⓵3種+ ⓶1種+⓷1種+⓸2種)×2パターン=14種類、である。④と⑤では、物理パラメータを3パターン考慮するので、21種類存在する:(⓵3種+ ⓶2種+⓸2種)×3パターン=21種類、である。提案手法は、①~③では(❶2種類+❷2種類)×2パターン=8種類、④と⑤では(3パターンなので)12種類である。
1⃣ 実際の比較結果
大きな傾向を示すため、①~⑤について、相対L2誤差が10-3である割合、10-2である割合・・・等を示す。最高性能を示した組み合わせも、併せて示す。
① 既存手法:10-4|0.00%、10-3|7.14%、 10-2|28.57%、10-1|50.00%、100|14.29%
提案手法:10-4|0.00%、10-3|50.00%、10-2|50.00%、10-1|0.00%、 100|0.00%
最高性能は、❷with㊂である。
② 既存手法:10-4|0.00%、10-3|35.71%、10-2|28.57%、10-1|35.71%、100|0.00%
提案手法:10-4|0.00%、10-3|62.50%、10-2|37.50%、10-1|0.00%、 100|0.00%
最高性能は、実は、⓸with㊂である。
③ 既存手法:10-4|0.00%、10-3|42.86%、 10-2|0.00%、10-1|57.14%、100|0.00%
提案手法:10-4|0.00%、10-3|100.00%、10-2|0.00%、10-1|0.00%、 100|0.00%
最高性能は、⓶である。
④ 既存手法:10-4|14.29%、10-3|38.10%、10-2|23.81%、10-1|23.81%、100|0.00%
提案手法:10-4|33.33%、10-3|33.33%、10-2|33.33%、10-1|0.00%、 100|0.00%
最高性能は、❶with㊂ である。
⑤ 既存手法:10-4|14.29%、10-3|38.10%、10-2|33.33%、10-1|14.29%、100|0.00%
提案手法:10-4|33.33%、10-3|33.33%、10-2|33.33%、10-1|0.00%、 100|0.00%
最高性能は、❶with㊂ である。
2⃣ 小括
最高性能だけを取り上げると、既存手法でも遜色がないように見えるかもしれない。しかし、”安定性”で捉えると、相対L2誤差が、10-2で収まっている提案手法に軍配が上がる。とは言え、物理系を変えて、さらに物理パラメータを変えると、違った景色が見えてくるはずなので、提案手法が飛び抜けて優秀ということではない(だろう)。
(3) ❶と❷の比較
一概には言えない(ところが悩ましい)。①及び②では、❷with㊀の性能が著しく低い。③~⑤では、その傾向は見られない。また、①~③では❷with㊂の性能が最も高い。④~⑤では、ほぼ❶with㊂の性能が最も高い。
オプティマイザで言えば、㊀よりも㊂の性能が、ほぼ高い。
【5】[*88]の構成
(0) 概要
[*88]で行いたいことは、以下である:(バーガース方程式、アレン=カーン方程式)×(物理パラメータ、初期条件、コロケーション点数、再サンプリングの回数)という、多種多様な組み合わせに対して、6つのサンプリング手法を適用する。どの組み合わせに対しても、「相対L2誤差が小さい」サンプリング手法があれば、それを発見する。
なお[*88]では、損失関数=データ損失+PDE損失+境界損失とした上で、「順問題なのでデータ損失は考慮しない」、「境界損失にはハード制約を課す」ので、最適化計算の対象はPDE損失のみである。ここでの境界損失は、初期損失を含む(含んでも良い)。
(1) サンプリング手法
6つのサンプリング手法を適用する:⓵一様ランダム分布に従うサンプリングを行う。⓶Hammersleyサンプリング†12を行う。⓷”現時点”の残差等を反映した確率分布関数に従うサンプリングを行う。ただし、初期分布はランダム分布。⓸基本的に⓷と同じ。違いは、初期分布のみで、初期分布からのサンプリングはHammersleyサンプリングに従う。⓹”現時点”の推定解の2次導関数(空間微分と時間微分の混合微分:∂2/∂t∂x)を反映した確率分布関数に従うサンプリングを行う。⓺”現時点”の残差の2次導関数に基づく(つまり、∂2/∂t∂x)を反映した確率分布関数に従うサンプリングを行う。
†12 ディスクレパンシー(discrepancy)が小さい擬似乱数”数列”である、Hammersley点群を使ったサンプリング。Hammersley点群は、有限個の点から成るため、数列と呼ばず点群と呼ぶ(らしい)。ディスクレパンシーが小さい数列の他例として、Halton数列、Sobol数列、GFSR(Generalized Feedback Shift Register)数列、Good Lattice点群などがある。ディスクレパンシーとは、乱数の均一さを表す尺度である。その値が小さいほど、乱数は均一である(つまり、真の乱数に近い)。Hammersley点群のディスクレパンシーは、Halton数列より小さい(らしい)。
(2) 検証に用いた物理系のセットアップ
①1次元バーガース方程式。コロケーション数2,000。物理パラメータν=π/100。初期条件u(x,0)=-sin(πx)。再サンプリングを{10,20,30,40,50,75?,100}回実施。
②1次元バーガース方程式。コロケーション数{250,300?,500,750,1000,2000}。物理パラメータν=π/100。初期条件u(x,0)=-sin(πx)。再サンプリングを100回実施。
③1次元バーガース方程式。コロケーション数2,000。物理パラメータν=π/100。初期条件は、3つの低周波数正弦関数を、ランダムに重み付けした関数をu(x,0)とする。再サンプリングを{10,20,30,50,100}回実施。
④1次元バーガース方程式。コロケーション数2,000。物理パラメータν=π/100。初期条件は、4つの高周波数正弦関数を、ランダムに重み付けした関数をu(x,0)とする。再サンプリングを{10,20,30,50,100}回実施。
⑤1次元バーガース方程式。コロケーション数2,000。物理パラメータν=π/100。初期条件は、u(x,0)=sin(2πx)†13。再サンプリングを{10,20,30,50,100}回実施。
⑥1次元バーガース方程式。コロケーション数2,000。物理パラメータν=π/100。初期条件は、u(x,0)=1.5×sin(πx)†14。再サンプリングを{10,20,30,50,100}回実施。
⑦1次元バーガース方程式。コロケーション数2,000。物理パラメータν=0.01。初期条件u(x,0)=-sin(πx)。再サンプリングを{10,20,50,100}回実施。
⑧1次元バーガース方程式。コロケーション数2,000。物理パラメータν=0.001。初期条件u(x,0)=-sin(πx)。再サンプリングを{10,20,50,100}回実施。
⑨1次元バーガース方程式。コロケーション数1,000。物理パラメータν=0.01。初期条件u(x,0)=-sin(πx)。再サンプリングを{10,20,50,100}回実施。
⑩1次元バーガース方程式。コロケーション数4,000。物理パラメータν=0.001。初期条件u(x,0)=-sin(πx)。再サンプリングを{10,20,50,100}回実施。
⑪アレン=カーン方程式。コロケーション数500。物理パラメータD=0.001。初期条件u(x,0)=x2cos(πx)。再サンプリングを{20,30,50,100}回実施。
⑫アレン=カーン方程式。コロケーション数1,000。物理パラメータD=0.001。初期条件u(x,0)=x2cos(πx)。再サンプリングを{20,30,50,100}回実施。
⑬アレン=カーン方程式。コロケーション数2,000。物理パラメータD=0.001。初期条件u(x,0)=x2cos(πx)。再サンプリングを{20,30,50,100}回実施。
†13 [*88]では、u(x,0)=sin(2π)となっているが、それでは恒等的に0なので、sin(2πx)とした。
†14 [*88]では、u(x,0)=1.5×sin(π)となっているが、それでは恒等的に0なので、1.5×sin(πx)とした。
(3) ハイパーパラメータ等
Adamの学習率・・・1.0×10-3
隠れ層の数・・・3
隠れ層のニューロン数・・・64
活性化関数・・・tanh(双曲線正接関数)
LBFGS適用のタイミング・・・Adamの初期 15,000 ステップに続いて LBFGS の 1,000 ステップ。その後 2,000ステップごとに再サンプリング。再サンプリングは、最初の1,000ステップがAdamで、続く1,000ステップが LBFGS。
【6】[*88]の検証結果
(1) 比較指標
比較指標である相対L2誤差は、異なるランダム・シードを用いた20回の学習過程にわたる平均値として算出されている。
(2) 比較検証の結果
①→ 相対L2誤差の水準は、良くて、10-4~10-3。⓵⓶が全くダメで、⓷は不安定、⓹がやや悪く、⓸と⓺が良い結果。
②→ 相対L2誤差の水準は、良くて、10-4~10-3。⓶はコロケーション点の増加に対する相対L2誤差の向上感度が鈍感。⓷と⓹は類似の挙動をとる。コロケーション点が1,000を越えてから急速に、敏感になる。対照的に、⓺はコロケーション点の数が少ない状況で敏感で、1,000を越えてから鈍感になる。⓵⓸は評価対象外。
③~⑥→ 相対L2誤差の水準は、良くて、③で10-2、④で100、⑤で10-3、⑥で10-32。⓵⓶は、再サンプリング回数を増やしても相対L2誤差が改善しない。④は、壊滅的に精度が低いが、⓺が最良であることに変わりはない。⓺が最良である傾向は、⑤で顕著。⓸は、なぜか評価対象外。
⑦~⑧→ 相対L2誤差の水準は、⑦で10-4に達している。⑧では、10-1に留まる(物理パラメータの影響大)。ここでも、⓺が最良である。
⑨~⑩→ ⑨~⑩における相対L2誤差の水準議論は、本質的に⑦~⑧と同じであるので省略。ここでも、⓺が最も優れた性能を示している。
⑪→ 相対L2誤差の水準は、10-2程度である。⓵⓶は全くダメである。加えて⓵⓶は、再サンプル回数を増やしても、相対L2誤差は全く改善しない。ここでは、⓺の性能は最良とは言えず、代わりに⓸が最良となる。なお⑫及び⑬に関しては、結果が明示されていないが、⑪と同じ傾向であると記されている。
(3) 小括
バーカース方程式の範疇では、色々いじってみても、⓺が最も優れている。しかし、アレン=カーン方程式になると、⓸が最良と言える。ただ、再サンプリング回数が30を越えて以降は、ほぼ最良と考えても良いように思う。つまり、全ての組み合わせで⓺が最も優れている、と言っても良いように思える。[*88]も、そのように結論付けている。
【7】考察と感想
(1) [*87]の考察等
1⃣ 本質的に重要な点は、確率分布に従ってサンプリングすることでコロケーション点を"間接的に"構成するのではなく、”直接”構成するという新しい方法論を示したことであろう。その上で、学習が安定していることを示した。”物理パラメータの広い範囲で、相対L2誤差が小さい”ことは、代理モデルとしては、肝であろう。学習が安定しているとは、物理系及び物理パラメータの『広い範囲』で、相対L2誤差が小さい、ことを指している。安定化のメカニズムは、カリキュラム学習のそれと同様と考えられるだろう。
2⃣ オプティマイザの影響は、やはり大きい。[*87]の結果だけを見ると、LBFGS単体は、ありえない。Adamを第一選択として良いが、多くの場合でAdam+LBFGSを採用することより、精度向上が期待できる。
3⃣ PINNsの相対L2誤差の相場感は、良くて10-4~10-3であることがわかる。
4⃣ [*87]の方法と、エネルギー自然勾配法と組み合わせて、幅広いケースでシミュレーションした結果が見たい。
5⃣ 数値計算でも、気を遣う点というか工夫する点は多々ある。代理モデルの構築においても、それは変わらないと諦念すれば、面倒には思えないかもしれない。もっとも、ツール化されれば、手間ではないだろう。
(2) [*88]の感想
1⃣ [*88]は、問題の根っこを特定して、解決したという内容ではない。対照的に[*87]は、(真実か否かは分からないが)問題の根っこを特定して、解決したという内容である。肚に落ちるし、汎用性が高いと感じる。
70種類を越えるとされる認知症の中で、最も大きな割合を占めるとされているのが、アルツハイマー型認知症(以下、アルツハイマー病)である†1。アルツハイマー病の発症原因は、完全には解明されていないが、アミロイドβ(ベータ)並びに、タウ・タンパク質(以下、タウと略す)が大きな役割を果たしていると、強く信じられている🛡。タウが発症に関わるとされる疾患†2では、その濃度が脳の特定部位で過剰になり、ミス・フォールドしたタウが積み重なって、神経原線維変化(neurofibrillary tangles; NFT)を形成する。このミス・フォールドしたタウの時空間パターンは、タウ濃度を変数とする反応拡散方程式に従うことが、示唆されている。
米ブラウン大学と米スタンフォード大学の研究者は、「PINNsとシンボリック回帰を使って、アルツハイマー病の早期診断モデルを構築した」とする論文[*93](以下、本論文)を発表した(23年7月16日@arXiv)☛【2】(0)を参照。
†1 67.6%という数字が示されることが多い。出典は、[*94]。ただ、これはデータが古い(平成24年。しかし、令和元年の厚生労働省資料[*95]にも引用されている)し、面接調査で診断が確定した”わずか”978 名の内訳に過ぎない。もう少し新しく、患者数も多い(23,484名)調査だと58%という数字がある[*96]。いずれにしても、太宗を占めること自体に、変わりはなさそうである。ただし、若年性認知症では、脳血管性認知症の割合の方が高い[*97]。
†2 タウオパチーと呼ばれる。
🛡 アミロイドβがアルツハイマー病の原因であることを示唆した2006年の論文@natureの撤回について、同意がなされた(24年6月4日[*101])。画像データが改竄されていたためである。脳からアミロイドβを除去することで、アルツハイマー病の症状を改善しようとする試みは、ほぼ全て失敗した(エーザイの「レカネマブ」が唯一の例外)。「アミロイドβがアルツハイマー病を引き起こす」という有力な仮説に対する疑問への、新たな裏付けとなるかもしれない。
【1】本論文の主張
本論文は、以下を主張する:PINNsとシンボリック回帰を組み合わせることで、アルツハイマー病における、ミス・フォールドしたタウ濃度を説明する、反応拡散方程式を発見できる。
【2】事前整理
(0) 本論文でやっていることの事前整理
1⃣ PINNsによる反応モデルの推論
PET画像は、脳内のミス・フォールドしたタウの濃度を抽出し、追跡することを可能にする。 本論文では、ADNI†3データベースから抽出した、被験者76名のタウ濃度データを用いる。タウ濃度が従う方程式(支配方程式)を損失関数に埋め込むPINNsを使って、タウ濃度と反応モデルを、ニューラルネットワーク(NN)で近似する。反応モデルとは、反応拡散方程式の”反応項”を指している。本論文では、反応モデル(反応項)に対して、関数形を仮定せずに、推定する(NNで近似する)。形式上、2種類の物理量をNNで近似していることに注意。
2⃣ シンボリック回帰による表現式の推論
NNで近似された反応モデルに対して、シンボリック回帰を適用して、タウ濃度に関する表現式(関数)を推定する。この関数が異なることをもって、母集団をアルツハイマー病患者と健常対照群とに分別する。
†3 ADNI(Alzheimer’s Disease Neuroimaging Initiative)は、アルツハイマー病発症過程を縦断する脳画像研究[*98]であり、日本、米国、欧州、豪州において、同一プロトコルを用いて実施される、非ランダム化長期観察研究である。2005年に米国で発案、開始された[*99]。日本のADNIは、J-ADNIと呼ばれる。
(1) タンパク質のミス・フォールディングと神経変性疾患の発症
細胞内の小器官リボゾーム(リボソーム)で翻訳・合成されたタンパク質は、アミノ酸が直線状に繋がったひも状の構造をしている。折りたたまれるのは、小胞体においてである。折りたたまれること(フォールディング)によって、ネイティブ構造と呼ばれる固有の立体構造を得る。フォールディングによって、タンパク質は、固有の機能を正しく獲得する。
正しくフォールディングできない、あるいは、正しくフォールディングしたあとで変性することを、ミス・フォールディングと呼ぶ。ミス・フォールディングしたタンパク質は、期待される役割を果たさないので、不要物(言葉を選ばなければ、ゴミ)である。本来、不要物であるミス・フォールディングしたタンパク質は、酵素によって分解されるが、分解機構が何らかの理由で破綻すると、不要物が凝集・蓄積する。そして、凝集・蓄積した不要物は、細胞死を引き起こし、神経変性疾患を発症する†4。
つまり、タンパク質がミス・フォールディングしただけでは、発症しない。排泄する仕組みが破綻して初めて、発症する(はずである。単に処理能力を越えるだけという解釈も可能だろうが、おそらく、それほど単純ではないはず。ただし、本稿は、そこには立ち入らない)。
†4 生体内の不要物は、機能を果たさないだけで留まれば良いが、なぜか悪さをする。
(2) シンボリック回帰
一般に、データから関数を推測することをシンボリック回帰と呼ぶ。シンボリック回帰では、一方で加減乗除を用意し、他方で解析関数を用意する。それらをランダムに組み合わせることで、データの入出力関係に適合する関数を見つける(もちろん"関数"は、入力変数のn次多項式を含む)。アルゴリズムとしては、遺伝的アルゴリズムやニューラルネットワークが使用される。
【3】本論文におけるセットアップ
(0) 2つのステップが必要である理由
本論文は、アルツハイマー病の早期診断モデルを構築する。早期診断とは、アルツハイマー病患者と健常対照群を分別することを指している。分別は、ミス・フォールドしたタウの濃度を記述する表現式が異なることを根拠として、行う。表現式は、二つのステップを経て、推論する。1⃣第一ステップでPINNsを使い、2⃣第二ステップでシンボリック回帰を使う。
なぜ、2つのステップが必要かというと、 陽電子放出断層撮影(Positron Emission Tomography:PET)画像は、高い空間分解能を持っている反面、時間分解能は低く、時間内の数点のみに限定されているからである。つまり、時間的情報が疎ら過ぎるため、PET画像から抽出したタウ濃度から直接、シンボリック回帰によって、表現式を推測することはできない。
(1) グラフ上で離散化した反応拡散方程式
脳のコネクトーム†5におけるミス・フォールドしたタウの凝集と伝播を、反応拡散方程式で表す。反応拡散方程式は、次のような形をした偏微分方程式である。
∂c/∂t=拡散係数∆c+f(c)
この偏微分方程式をPINNsで扱えるように、重み付き無向グラフG上で離散化する。この場合のグラフ(脳グラフ)Gのノードは、重複しない異なる脳領域を、エッジは、異なる領域間の軸索†6接続を表す。具体的な脳グラフは、ブダペスト・リファレンス・コネクトームv3.0†7から、取得する。オリジナルの脳グラフには、1,015個のノードがあるが、これを83個の縮小させた。この83個のノードは、83 個の皮質および皮質下の脳領域と考えられる。
離散化した支配方程式は、以下のようになる(ここにオリジナリティはない)。
dci/dt=-κ∑jLijcj+αf(ci)
ciは、領域iのタウ濃度。κは拡散係数、αは反応係数。Lijは、グラフ・ラプラシアン†8である。i及びjは、全てのノードに渡る(つまり、本論文では1~83)。PINN 推論段階で10回の独立したシミュレーションを実行して、被験者ごとに10 個の異なる「パラメーター セット{κ、α}及び反応モデルf」、を取得する。
†5 神経系内各要素間の詳細な接続状態を表した”地図”をコネクトームと呼ぶ。
†6 (神経)軸索は、神経細胞の細胞体から延びる突起状の構造を有し、他神経細胞への情報の出力を担う。
†7 ブダペスト・リファレンス・コネクトーム・ヴァージョン3.0は、477人のコネクトームから得られたパラメータ化可能な(コンセンサス)脳グラフ。477人のコネクトームは、ヒューマン・コネクトーム・プロジェクトのMRIデータセットから計算された。脳グラフは、サイト(https://pitgroup.org/connectome/)からダウンロードできる。
†8 グラフ・ラプラシアンL=次数行列Dー隣接行列A、である。
(2) 損失関数
本論文のPINNsでは、損失関数は、データ損失+PDE損失+補助損失、で構成される(初期損失・境界損失はハード制約されるので、最適化計算の対象たる損失関数には現れない)。本論文の支配方程式である反応拡散方程式は、拡散項と反応項で構成される。拡散項は既知(パラメータは未知)、反応項は未知である。従って、このケースはPINNsの文脈で言うと、形式上、逆問題と見做すことができる(だろう)。従って、 データ損失が考慮されているという解釈が可能である(と思われる)。
また補助損失(正則化項)は、反応拡散方程式は進行波解を持つことを保証する条件を、ソフト制約として課す役目を果たしている。
なお、オプティマイザはAdam+L-BFGSが使用されている。
(3) シンボリック回帰
1⃣ 概要
本論文では、(本論文の著者の一人が所属する)米スタンフォード大学が開発したPySRが使用されている†9。PySRは、Juliaバックエンド SymbolicRegression.jl上に構築されたPythonインターフェイスを備えたオープンソース・ソフトウェアである。PySRは、遺伝的アルゴリズム・ベースのシンボリック回帰である(ほとんどが、そうであると言っても良い)。
2⃣ 評価方法及び、評価指標
シンボリック回帰から発見された式(以下、表現式とする)を評価する指標として、スコア=-δlog(MAE)/δℭが使用された。MAEは平均絶対誤差、ℭは式の複雑さを表す。δは局所的な変化を表している†10。
損失が少なくスコアが高いモデルが好ましいので、損失とスコアのバランスをとる。具体的には、損失については、最小値の5割増しまでを許容範囲する。つまり、損失最小のモデルにおける損失を1.5倍した値より、損失が大きくないモデルは候補として残す。この時点で「パラメータ{κ、α}及び表現式」のセットが残る。
次に、表現式を一つに絞り込むため、射影誤差という指標を導入する。射影誤差は、本質的に||実際のタウ濃度c(t)ー推定タウ濃度c'(t)||2で表される(ノルムはL2ノルム)。c'(t)は、表現式を反応項として代入した反応拡散方程式の解である†11。射影誤差が最小の表現式が、最終的に選ばれる。
†9 シンボリック回帰(SR)用ツールには、他にも、SINDy、Eureqa、AI Feynman、AI-Descartes等がある(まだまだ沢山ある)。なお、23年7月@arXivの論文[*100]は、「実世界のデータでしばしば直面する一般的な課題に対して、SRがどの程度有効であるかを評価するために、合成データセットと実世界のデータセットからなるコンペティションを開催した」結果をまとめた論文である。唯一無二のツールはない、というのが結論である。ただ、ざっくり言って、PySRは優秀な成績を修めていると思う。
†10 本論文では、∆という記号が使われているが、ラプラシアン(∇2)と紛らわしいので、δを使った。
†11 グラフ上で離散化した反応拡散方程式(常微分方程式)は、scipy.integrate.odeintを使って解いた。
【4】結果
(0) 予備テスト
1⃣ セットアップ
まず、PINNs+シンボリック回帰が、ミスフォールドしたタウ濃度を表現する式を構築できるか、についてテストを行った。具体的には、初期条件・パラメータ・反応項を変化させた、タウ濃度のシミュレーションが実行された。
i 番目のノード(すなわち脳領域)の初期タウ濃度(初期条件)は、実際のデータと同等の平均と分散を持つ正規分布からサンプリングされた。パラメータκ及びαは、適当な平均と分散を持つ正規分布に従うと仮定された。被験者は、4グループに分けられ、それぞれ異なる反応モデル:Fisherモデル(①c(1 − c))、Newell-Whitehead-Segelモデル2種(②3√3c(1ーc2)/8、③22/3c(1ーc3)/3)、Zeldovich-Frank-Kamenetskiiモデル (④(2+√5)c(1ーc)exp(cー1ー(ー3+√5)/2)/4)、が割り当てられた。グラフ・ラプラシアンは、実際のデータと同一になるように設定された。タウ濃度c(tk)は、k = 0、1、2 年に対して、 tk = k でサンプリングされる。
最後に、パラメーター κ と α およびは反応モデルを特定した後、それらをグラフ上で離散化した反応拡散方程式(常微分方程式)に代入し、scipy.integrate.odeintを使用して解いた(期間は20年)。そうすることで、モデルの予測可能性を調べた。
2⃣ テストの結果
4パターンの反応モデルをシンボリック回帰した結果は、ほぼ正確である。①は、c(1 − c)が、(1ー0.01c)×c(1ーc)とシンボリック回帰された。つまり1→1ー0.01cである。②は、3√3c(1ーc2)/8が、0.65c(1ーc2)である。つまり、3√3/8≒0.6495→0.65である。③は、22/3c(1ーc3)/3が、0.53c(1ー1.019c3)である(1.019は、概数値)。つまり、22/3/3≒0.529→0.53、かつ1→1.019(=54/53)である。④は、(2+√5)c(1ーc)exp(cー1ー(ー3+√5)/2)/4が0.58c(1ーc)exp(c)である。つまり、(2+√5)exp(ー1ー(ー3+√5)/2)/4≒0.5708→0.58である。
最終的なタウ濃度の予測結果(反応拡散方程式を解いた結果)†12とグランドトルゥースとの比較は、図示されているのみである。図を見る限り、一致精度は高い。
†12 嗅内皮質、中側頭回、上側頭回という3つの異なる脳領域において行われた。正確には、それぞれ左と右があるので、6つの領域ということになる。嗅内皮質は、海馬と共に記憶に深く関わる脳領域とされる。側頭葉を構成する頭回の一つである中側頭回は、視聴覚情報の統合を担っていると考えられている。(同様な)上側頭回は、聴覚を担うとされる(一次聴覚野がある)。
(1) 実データによる結果
76 人の被験者は 2 つのグループに分類された。46 人は、平均アミロイド濃度が一定レベルを超えることを意味する、アミロイド陽性(Aβ+)として識別され、30 人はアミロイド陰性 (Aβ-) として識別される。
Aβ+=アルツハイマー病患者の反応モデルf+(c)は、 f+(c) = 0.23c3−1.34c2+1.11cと推定された。Aβ-=健常者の反応モデルf-(c)は、f-(c) = −c3 + 0.62c2 + 0.39cと推定された。図で表すと、f+(c)は、タウ濃度が薄い段階で(つまり早い段階で)立ち上がっていることがわかる(これは、アルツハイマー病患者は、タウ濃度が低い段階で、タウのミス・フォールディングが発生していると捉えて良いのだろうか?)いずれにしても、f+(c)とf-(c)は識別できる(と見做して良いだろう)。
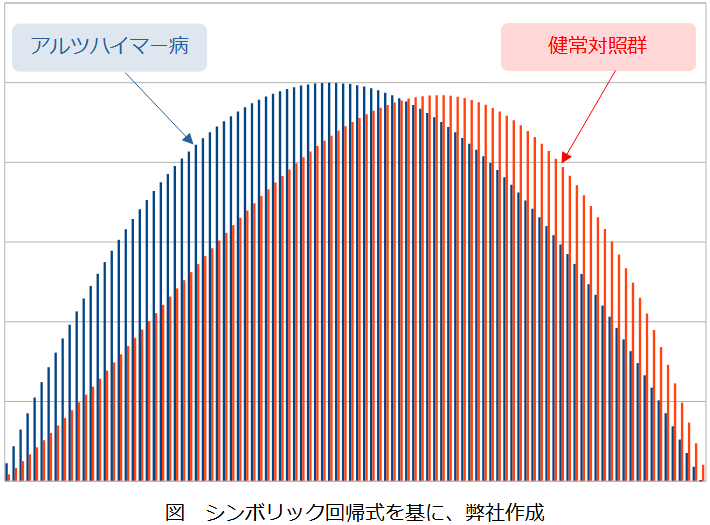
それぞれの反応モデルを代入した(グラフ上で離散化された)反応拡散方程式を解いた。期間は30年。
(テストデータと同様に)被験者36人がランダムに抽出された。脳領域も同様に、嗅内皮質、中側頭回、上側頭回という3つの領域が対象である。さらに左右の区別があるので、正確には、6つの領域が対象となっている。実データの場合は、PINNs+シンボリック回帰の結果が、どれほどバラついているかを図示している。つまり、予測結果の「最大値・最小値及び、最良値」を30年間にわたり図示している。おおむね5/6は、バラつきが小さい(安定した予測ができている?)と見做せるだろう。
【5】考察
(0) Fisherモデルは別として、Newell-Whitehead-Segelモデル、Zeldovich-Frank-Kamenetskiiモデルは、そこそこ複雑な形をしているが、シンボリック回帰は見事に成功している。
(1) PINNsの新しい可能性が示されたのかもしれない。データが少ないあるいはノイズが大きいため、直接的にはシンボリック回帰が適用できないケースでも、PINNsを併用することでシンボリック回帰可能であれば、新しい機会が生まれる。説明可能な深層学習フレームワークが望まれる時世なので、今後適用例が増えるかもしれない。
(2) 本論文では、偏微分方程式(反応拡散方程式)をグラフ上で離散化した常微分方程式(系)を埋め込んだPINNsを使用している。ブダペスト・リファレンス・コネクトームを使って、脳グラフを利用できるため、実行可能なフレームワークである。数理的には、シグネチャや圏論を使った解析も可能であろう(が、特段のメリットは無いかもしれない)。
韓国・中央大学の研究者は、「実世界の最適化逆問題をPINNsで解いてみた」論文[*109](以下、本論文)を発表した(24年1月8日@scientific reports)。PINNsによる結果を、遺伝アルゴリズム(GA)や強化学習(RL)と比較している。
最適化逆問題とは、制約条件の下で、目標を達成する最適なパラメータを選ぶという問題である。 最適化逆問題は従来、変分法やGAで解かれていた。機械学習モデルの発展とともに、強化学習が適用されるケースも増えてきた。そういった背景の下、PINNsで解いたらどうかなるか、という論文である。
【1】本論文の主張
本論文は、╏対象╏の最適化逆問題において 以下を主張する:
(1) PINNsは、GAやRLよりも、少ない探索で(つまり、速く)最適解に到達する。
(2) PINNsは、GAやRLでは困難な、”狭く不安定な解”(☞【2】(2)❸を参照)を取得することができる。
╏対象╏ 自然法則に従っている物理系。つまり、支配方程式が明示できる物理系(☞【2】(1)を参照)。
【2】本論文のポイント
(1) 具体的な対象
自然法則に従っている物理系が最適化問題の対象である。従って、スポーツリーグやトーナメントのスケジュール作成問題やポートフォリオ最適化問題などは、対象外である(と合理的に推論できる)。また、支配方程式が明確になっている物理系を扱っている。本論文では、支配方程式が明確になっていない物理系の例として、核融合炉が上げられている。
(2) 問題のセットアップ
具体的に対象となった最適化逆問題は、以下の通りである:振り子の反転、最短時間経路の探索(2件)、宇宙船のスイングバイ軌道探索。
❶ 振り子の反転
固定軸振り子の振り上げは、コントローラーのパフォーマンスをテストするためのよく知られた問題らしい。ある固定時刻に、振り子を”垂直反転状態”にする、(アクチュエータの)トルク・シナリオを見つけることが、この場合の最適化逆問題となる。なお固定時刻は、10秒に設定されている。トルクの大きさには、制限が課されている(ので、1回のスイングで垂直反転状態にすることはできない)。
支配方程式は、運動方程式である。制約は、「トルクの大きさが制限されている」ことである。目標は、「ある固定時刻に、振り子を垂直反転状態にする」ことである。
❷ 最短時間経路の探索
最短経路を探索するという、この最適化逆問題は、本論文では2件取り上げられている:㈠屈折率が異なる媒体を通過する光の最短経路を探索する問題、㈡重力下での 2 つの特定の点間の最短時間降下経路を探索する問題。
㈠を規定する物理法則は、フェルマーの原理🐾1として知られている。制約は、「始点と終点の座標が定められている」ことである。目標は、最短時間で終点に到達することである。
㈡を規定する物理法則は、エネルギー保存則である。制約及び目標は、㈠と同じである。
🐾1 フェルマーの最終定理で有名な、ピエール・ド・フェルマーの名が冠されている。
❸ 宇宙船のスイングバイ軌道探索
(宇宙船の)スイングバイ軌道とは『宇宙船が、複数の天体から受ける重力を利用して、搭載燃料を使用せずに、目標位置に到達する経路』を指す。ここでの、最適化逆問題とは、スイングバイ軌道の探索である。この問題では、最適な経路からのわずかな逸脱でも、宇宙船に作用する重力が敏感に変化し、星に墜落するようなまったく異なる経路と目的地になる可能性がある。これが、本論文で言うところの、”狭く不安定な解”である。
支配方程式は、運動方程式。制約は、「始点と終点の座標が定められている」ことである。目標は、「目標位置における推力がゼロになる」ことである。
(3) 損失関数
本論文ではPINNsに対して、「様々な条件を損失関数として取り入れることができる」という柔軟性が、PINNsの出色であることを改めて指摘している。本論文では、PINNsにおける損失関数を、「物理損失、制約損失、目標損失」と分別呼称している。物理損失は、PINNsにおける普通の用語で言い換えれば、PDE損失である。制約損失は、PINNsにおける普通の用語で言い換えれば、境界損失である。目標損失は、逆問題用の損失関数という理解で良い。
❶では、制約損失は、時刻t=0で{角度, 角速度, トルク }={0, 0, 0}である。目標損失は、(cos φ(t=10秒) -(−1))2である。
❷では、制約損失は、適当に定めた、始点と終点の座標である。目標損失は、最短時間経路を通過する時間Tである。
❸では、制約損失は、適当に定めた、始点と終点の座標である。目標損失は、物理損失の中に組み込まれているというか、同一である。❸における目標損失に該当するのは、運動方程式における外力(この場合、推力)である。目標は、推力を目標位置においてゼロにすることであり、時間発展を記述する必要があるが、これはまさに、空間位置の2階時間微分で捕捉することができる。つまり運動方程式で捕捉すればよい。一方で、PINNsのいわゆるPDE損失(本論文で言う、物理損失)は、支配方程式=0の形式なので、「空間位置の2階時間微分ー外力=0」の形式にする必要があるが、これはまさに、目標損失と同じである。
(4) 強化学習の報酬
強化学習の報酬Rは、❶では R = −(cos φ -(−1))2に設定された。反転時、つまり角度が180°の場合、cos(180°)=-1である。
❷では、R = −wTT − ((x − x1)2 + (y − y1)2)に設定された。ここで、wTは係数であり、❷㈠では0.01、❷㈡では10と設定された。{x1、y1}は、終点の座標である。
❸では、R = −平均(|推力|2) − ((x − x1)2 + (y − y1)2)に設定された。{x1、y1}は、目標位置の座標である。
(5) なぜ、PINNsのパフォーマンスが良いか。
全ての最適が逆問題でPINNsのパフォーマンスがより優れているわけではない。本論文の最適化逆問題は、あくまで自然法則が備わっている物理系かつ、支配方程式が明確に規定されている場合に限定されている。この限定されたケースで言うと、PINNsは自然法則を知っている(ように学習が行われる)。このため、PINNs は (GAやRLとは異なり) 探索的な試行錯誤を通じて、環境について学習するわけではない。支配方程式を通じて、直接(試行錯誤的ではない、という意味)、環境について学習する。故に、学習速度が速いことは、当然と言えるだろう。
一方で、GAやRLは、自然法則を知らない(自然法則を教わることなしに、学習が行われる)。機械学習寄りの言葉を使えば、ドメイン知識がない、という状況で学習しているのだから、収束が遅い(及び、必ずしも最適解に到達しない)のは、当然であろう。GAやRLでは、あくまで、最適化逆問題を、最終状態に到達するまで積み重なる「一連の時系列アクションに対する応答タスク」として扱う。その後、それらのタスクを通じて、ポリシーを調整する。
RL は、さまざまな状態で対話型の意思決定が必要なリアルタイム制御、あるいは競争ゲームにおいては、PINNs よりも優れている。
【3】モデル・セットアップ
(1) ソフトウェア及びハードウェア環境
PINNs 実装には、DeepXDE ライブラリ🐾2を利用した。GA は、PyGAD🐾3を使用。RLは、Stable-Baseline3 ライブラリ🐾4で TD3 アルゴリズム🐾5を使用した。ハードウェアは、(NVIDIA)RTX-3080Ti GPU が使用された。
🐾2 当初、TensorFlow プラットフォームに基づいて、米ブラウン大で開発された。現在は(米ペンシルバニア大でメンテ、アパッチ・ライセンス)、PyTorch、JAX、PaddlePaddleなどの複数のバックエンドをサポートしている。ユーザーコードをコンパクトに保ち、 数学的定式化に近い形にすることが可能とされる。さらに、DeepXDEは、すべてのコンポーネントが疎結合であるため、構造化されており、高度に設定可能とされる。
🐾3 Pythonベースの有名なGAライブラリ。シンプルで使いやすく、細かい設定も可能とされている。
🐾4 Stable Baselines 3は、米オープンAIが提供する強化学習アルゴリズム実装セットOpenAI Baselinesの改良版。バックエンドはPyTorch。
🐾5 TD3(Twin Delayed DDPG)は、その名の通りDDPG(Deep Deterministic Policy Gradient)の改良アルゴリズム。DDPGは、アクター・クリティック・アルゴリズムであるが、方策の勾配計算を行わずに、パラメータが更新(最適化)される。アクターとは方策モデル(行動の選択、≃専門家の経験)を指し、クリティックとは、価値表現モデル(行動の価値評価、≃専門家の勘)を指す。
(2) モデルアーキテクチャ、ハイパーパラメータ
1⃣ PINNs
オプティマイザ・・・Adam+L-BFGS(順番に適用)
ノード数・・・64
隠れ層数・・・3
活性化関数・・・ ❶tanh、❷シグモイド関数、❸tanh
Adamの学習率・・・❶0.02、❷㈠0.001、㈡0.001、❸0.001
Adamのエポック数・・・❶5000、❷㈠2000、㈡2000、❸2000
L-BFGSの反復回数・・・❶4804回、❷㈠1232回、㈡2692回、❸1215回
グローバル重み(物理損失/制約損失/目標損失)・・・❶ 1/10/1、❷㈠ 1/1/0.01、㈡ 1/1/0.01、❸ 1/1/目標損失なし
※ スケジューリングなし、早期停止なし。重み初期化なし。
2⃣ RL
ノード数・・・64
隠れ層数・・・3
反復回数・・・105回
【4】比較結果
(0) 指標
定量的な指標は、モデル出力が最適化解=解析解に達する(あるいは、近づく)までの、現実世界での経過実測時間(elapsed wall time:EWT)である。5回アンサンブルの平均±標準偏差で表す。モデルの精度(出力と解析解との差)は、定性的に解釈されている。
なお、GAは❶のみ適用されている。RLは❶~❸に適用されている。
(1) ❶振り子の反転
EWT→PINNs=44±16秒。GA=4015±34秒。RL=892±10秒。
GAとRLは、解析解には到達していない。つまり、10秒後に垂直反転するトルクシナリオを見つけられていない。PINNsは、10秒後に垂直反転するトルクシナリオを見つけた。
(2) ❷最短時間経路探索
㈠ EWT→PINNs=45±29秒。RL=887±7秒。
RLは、解析解を再現出来ていない。PINNsは、解析解を再現した。
㈡ EWT→PINNs=36±11秒。RL=923±8秒。
RLは、解析解を再現出来ていない。PINNsは、解析解を再現した。
(3) ❸宇宙船のスイングバイ軌道探索
EWT→PINNs=62±17秒。RL=906±12秒。
RLは解析解を再現できたが、無駄な推力を使って目標位置に達している。一方、PINNsは、推力をほとんど使わずに、目標位置に達している。スイングバイ軌道は、推力を使わない軌道であるから、スイングバイ軌道を探索するというミッションには、RLは失敗している、と言える。
【5】感想
結果自体には、サプライズはない。PINNsの適用範囲が広がった、という印象。宇宙船のスイングバイ軌道探索は、インパクトがあるかもしれない(と感じる)。
米シンシナティ大学大学の研究者は、「バニラPINNsよりも、逆問題を速く解ける」新しいPINNsを提案した論文[*122](以下、本論文)を発表した(24年7月15日@arXiv)。本論文では、この新しいPINNsをDG-PINN(Data-Guided PINN)と呼んでいる。
特に、際立った研究でもない(?)ので、粒立てる必要もないだろうが、どの程度の差が出るかには興味がある、という趣旨。
【1】本論文の主張
様々な偏微分方程式(☞【3】(0)3⃣)に対する逆問題において、本論文は、以下を主張する:
(1) DG-PINNは、バニラPINNsと比べて、学習時間が短い(☞【3】(1)❶~(4)❶)。ざっくり言って。1/6程度に短縮される。
(2) バニラPINNsに対するDG-PINNの(性能の)優劣は、偏微分方程式によって異なる(☞【3】(1)❶~(4)❶)。
(3) DG-PINNは、ハイパー・パラメータの選択に関して堅牢である(☞【3】(1)❷~(4)❷)。
(4) DG-PINNは、ノイズ混入下でも、逆問題を正確に解くことができる。ただし、ナヴィエ・ストークス方程式を除く(☞【3】(1)❸~(4)❸)。
【2】DG-PINN
(1) DG-PINN概要
問題意識は、逆問題ⓍPINNsというセットアップにおおて、「PDE損失が急速に最小化される一方で、データ損失は高いままである(ケースが存在する)。その損失項間の不均衡が原因で、PINNの全体的な効率が低下する」である。解決策のアイデアはシンプルで、事前学習+再学習という2段階学習によって、不均衡を解消する。
事前学習では、データ損失項のみで構成される損失関数を最小化する。事前学習で最適化されたパラメータを初期パラメータとして、再学習を行う。再学習では、総損失関数=PDE損失+初期損失+境界損失+データ損失を最小化する(表記において、グローバル重みの記載を省略した)。グローバル重みは、動的に決定する(☞下記(2)1⃣参照)。
(2) DG-PINNの細部
本論文は逆問題を取り扱っているので、PINNsの損失関数にはデータ損失が含まれている。
1⃣ グローバル重みの算出
(総)損失関数のグローバル重みは、動的に調整される。つまり、適応型重みが採用されている。一般に、適応型重みの算出法として、勾配ベースと神経接核(Neural Tangent Kernel:NKT)ベースの2つの算出法がある🐾1が、本論文(DG-PINN)ではNKTベースを採用している。
2⃣ オプティマイザー
オプティマイザーは、Adam+L-BFGSである。正確には、データ損失のみを最小化する事前学習フェーズにおいてのみ、Adamを使用する。データ損失を含む総損失関数を最小化する「再学習」フェーズにおいて、L-BFGSを使用する。Adamでは、重みが1,000回の反復ごとに更新される。L-BFGSの重みは、固定である。Adam オプティマイザーの初期学習率は1.0×10-3、L-BFGSの学習率は0.1である。
🐾1 一般にNKTベースの重みは、勾配ベースの重みに比べてパフォーマンスが良いとされるが、計算コストが高い。
3⃣ ネットワークのセットアップ
隠れ層が100個のニューロンを持つ3層全結合ネットワークを使用する。活性化関数は、双曲正接活性化関数(tanh)である。ニューラルネットワークの初期化及び、偏微分方程式内の未知パラメータの初期化は、一様分布を用いて実現する。
【3】比較結果
(0) 全体像の整理
1⃣ 比較の全体像
❶性能評価、❷ハイパー・パラメータ選択に対する堅牢性、❸ノイズに対する堅牢性、を行っている。❶は、予測性能とパラメータ推定における性能(誤差が小さいこと)を評価する。下記2⃣を参照。❷は、事前学習フェースにおける、「最大反復回数M1🐾2及び、データ損失のデータポイント数Nd🐾3」という2つのハイパー・パラメータを使った感度分析を実施することで、堅牢性を評価している。❸は、データに白色ガウス雑音🐾4を混入させた場合の感度分析を実施することで、堅牢性を評価している。
🐾2 以下の15個で構成される:{2,000、3,000、4,000、5,000、6,000、7,000、8,000、9,000、10,000、15,000、20,000、25,000、30,000、40,000、50,000}
🐾3 以下の15個で構成される:{500、600、700、800、900、1,000、2,000、3,000、4,000、5,000、6,000、7,000、8,000、9,000、10,000}
🐾4 信号対雑音比(SNR)=40、35、30、25dB。ただし、ナヴィエ・ストークス方程式の場合のみ、SNR=40、35dB。
2⃣ 比較指標
比較指標は、L2相対誤差(単位:10-3)、APE(単位:%)、学習時間(単位:分)である。APEは、絶対パーセント誤差である。❶では、独立した10回の試行を実施して、各指標の平均値を算出している。
L2相対誤差は、バニラPINNsとDG-PINNの予測性能の比較指標である。APEは、逆問題の主題であるパラメータ推定における性能の比較指標である。下記(1)❶~(4)❶において、各比較指標を(バニラPINNs、DG-PINN)という順番で並列表記した。なお、ナヴィエ・ストークス方程式の場合、「L2相対誤差は、速度成分u及びvに対して計算」している。
3⃣ 対象とする偏微分方程式(まとめ)
1次元熱伝導方程式→(1)、1次元波動方程式→(2)、1次元オイラー・ベルヌーイ梁方程式→(3)、2次元非圧縮性ナヴィエ・ストークス方程式→(4)である。オイラー・ベルヌーイ梁方程式は、梁の曲げ運動を記述する方程式である。なお、本論文におけるナヴィエ・ストークス方程式は、円柱周りの流れを扱っている。
(1) 1次元熱伝導方程式
❶・・・L2相対誤差(1.05、1.44)、APE(0.05、0.14)、学習時間(26.83、4.26)。APEは、熱伝導係数の推定に対して計算されている。予測性能、パラメータ推定性能ともに、バニラPINNsが優れている、という結果。ただ、学習時間のみ、DG-PINNが優れている。
❷・・・全てのM1でL2相対誤差が小さいこと(6 × 10−3未満)及び、広範囲のM1に対して得られたAPEはすべて低い。このため、M1の選択に関して堅牢である、と結論されている。Ndに関してもL2相対誤差が小さいこと(4 × 10−3未満)及び、広範囲のNdに対して得られたAPEはすべて低い。故に、Ndの選択に関しても堅牢である、と結論されている。
❸・・・各ノイズに対して、L2相対誤差(単位:10−3)が1.47、2.25、4.47、9.67。APEは、0.16%、0.14%、0.24%、0.63%。これらの結果から、DG-PINNはノイズ混入下でも、1次元熱伝導方程式の逆問題を、正確に解くことができる、と結論されている。
(2) 1次元波動方程式
❶・・・L2相対誤差(1.30、0.749)、APE(0.003、0.003)、学習時間(28.57、4.57)。APEは、「係数=波の速度」の推定に対して計算されている。予測性能は、DG-PINNが優れているという結果。パラメータ推定性能は、バニラPINNsと同じという結果。学習時間も、DG-PINNが優れている。
❷・・・全てのM1でL2相対誤差が小さいこと(3 × 10−3未満)及び、広範囲のM1に対して得られたAPEはすべて低い。このため、M1の選択に関して堅牢である、と結論されている。Ndに関してもL2相対誤差が小さいこと(1.1× 10−3未満)及び、広範囲のNdに対して得られたAPEはすべて低い。故に、Ndの選択に関しても堅牢である、と結論されている。
❸・・・各ノイズに対して、L2相対誤差(単位:10−3)が0.659、1.16、2.00、3.63。APEは、0.002%、0.003%、0.007%、0.006%。これらの結果から、DG-PINNはノイズ混入下でも、1次元波動方程式を正確に解くことができる、と結論されている。
(3) 1次元オイラー・ベルヌーイ梁方程式
❶・・・L2相対誤差(0.410、0.262)、APE(0.01、0.10)、学習時間(38.04、6.43)。APEは、梁の材料特性に関連するパラメータの推定に対して計算されている。予測性能は、DG-PINNが優れているという結果。パラメータ推定性能は、バニラPINNsが優れているという結果。学習時間は、DG-PINNが優れている。
❷・・・全てのM1でL2相対誤差が小さいこと(3 × 10−4未満)及び、広範囲のM1に対して得られたAPEはすべて低い。このため、M1の選択に関して堅牢である、と結論されている。Ndに関してもL2相対誤差が小さいこと(3× 10−4未満)及び、広範囲のNdに対して得られたAPEはすべて低い。故に、Ndの選択に関しても堅牢である、と結論されている。
❸・・・各ノイズに対して、L2相対誤差(単位:10−3)が0.489、0.840、1.50、3.49。APEは、0.056%、0.065%、0.109%、0.852%。これらの結果から、DG-PINNはノイズ混入下でも、1次元オイラー・ベルヌーイ梁方程式を正確に解くことができる、と結論されている。
(4) 2次元非圧縮性ナヴィエ・ストークス方程式
❶・・・uのL2相対誤差(14.5、4.17)、vのL2相対誤差(61.7、16.6)、APE1(0.32、0.27)、APE2(13.83、2.29)、学習時間(58.12、6.80)。APEは、移流項に係る係数β1と粘性項に係る係数β2の推定🐾5に対して計算されている。APE1がβ1に該当し、APE2がβ2に該当する。予測性能及びパラメータ推定性能は、DG-PINNが優れているという結果。学習時間も、DG-PINNが優れている。
🐾5 ナヴィエ・ストークス方程式の移流項に、係数は付かない。本論文では、「逆問題として、パラメータを求める」というセットアップなので、形式上かつ無理やり、移流項に係数を付けている。実際、β1=1である。ちなみに、β2=0.01。つまり、動粘性係数=0.01と考えて良いだろう。これは、室温における水の値と考えて良いだろう。
❷・・・全てのM1でL2相対誤差が小さいこと(uについて6 × 10−3未満、vについて2 × 10−2未満 )及び、広範囲のM1に対して得られたAPEはすべて低い。このため、M1の選択に関して堅牢である、と結論されている。Ndに関してもL2相対誤差が小さいこと(uについて5 × 10−3未満、vについて2 × 10−2未満 )及び、広範囲のNdに対して得られたAPEはすべて低い。故に、Ndの選択に関しても堅牢である、と結論されている。
❸・・・各ノイズに対して、L2相対誤差(単位:10−3)がuについて5.70と10.6。vについて21.4と38.0。APEは、β1について0.076%と0.22%。β2について0.136%と8.89%。これらの結果から、DG-PINNはノイズ混入下でも、1次元オイラー・ベルヌーイ梁方程式を”解くことができる”、と結論されている。「β2の推定精度はノイズの影響を受けやすく、ノイズレベルが増加すると精度が大幅に低下する」ことが付言されている。
【4】考察
DG-PINNは、学習速度が6倍ほど加速される(ので、すごい)。性能が上がらないのは、驚くに当たらないだろう(↓)。
DG-PINNの性能星取表をまとめると、以下の通り:予測性能(L2相対誤差)4戦3勝1敗。パラメータ推定性能(APE)4戦1勝2敗1分け。
再生可能エネルギーの活用において、日本では地熱エネルギーが有望とされている。その理由としてあげられるデータは、日本が世界第3位(2,347万kW相当)🐾1の地熱資源大国という事実である。地熱エネルギーの持続的な利用には、地下における熱及び流体の流動に対する理解が不可欠であり、この理解は、地熱地域の自然状態🐾2モデル作成を通して進められる。少しだけ数理的な表現を使うと、この理解は、熱輸送と流体流動を連成させた問題をシミュレートすることによって進められる。
地熱地域の自然状態モデル作成には、シミュレーション結果を、現場での観測値(代表的には、温度と圧力)とキャリブレーションする必要がある。なお、言わずもがなであるが、このキャリブレーションは、逆問題を解くことに相当する。従来、このキャリブレーションには勾配法やベイズ推定法が適用されてきたが、勾配法やベイズ推定法は計算コストが高い。特に、熱流体連成シミュレーションのように、順方向問題が非線形である場合、計算コストはさらに高くなる可能性がある。そこで、「逆問題を解ける、計算コストが低い」計算フレームワークに対するニーズが、発生する。そのような計算フレームワークの代表例として、PINNsがあげられる。
京都大学他🐾3の研究者は、「地熱系🐾4の3次元逆問題解析🐾5において、PINNsの有効性を実証した」と主張する論文(以下、本論文[*126])を発表した(25年7月23日@Journal of Geophysical Research–Machine Learning and Computation)。ここでの、大きなポイントは、”3次元”というところである。本論文では、「PINNsの成功事例は、1次元および2次元問題に偏っていることが広く指摘されている」とした上で、地熱システムの地下数値モデルは、本質的に3次元である🐾6ため、「PINNsによる、自然状態地熱系の”3次元”における逆問題解析の有効性を実証することが不可欠である」という立場を堅持している。
🐾1 出典:https://www.chinetsukyokai.com/information/tokucho.html
🐾2 ☞【2】(1)を参照。
🐾3 九州大学、産業総合研究所、東北大学、米ローレンス・バークレー国立研究所。ただし、全て日本人。
🐾4 地熱資源が賦存する場を地熱系と呼ぶ。賦存とは、「潜在的には、存在している」という意味合いである。つまり、科学的な推論により、存在が強く推認される、という意味である。
🐾5 ☞【2】(1)を参照。
🐾6 ☞【2】(0)を参照。
【1】本論文の主張
本論文は、地熱系3次元逆問題解析に対して、以下を主張する:
(0) PINNsとは、相性が良い(☞【3】(0))。
(1) PINNsは、温度と流体圧分布に関してベースライン・モデル🐾7よりも予測精度が高い(☞【4】(1)1⃣及び2⃣)。
(2) PINNsは、透水係数に関して、ベースライン・モデルと同程度の予測精度であった(☞【4】(1)3⃣)。しかし、新しい損失項を追加することで、誤差は削減された(☞【3】(4)2⃣)。故に、PINNsの有効性が実証された。
🐾7 本論文では、「データ駆動型機械学習モデル」という文言が使われている。具体的なモデルについては【4】(0)2⃣を参照。
【2】事前整理
(0) 地熱系について
前述(☞🐾4)の通り、地熱資源が賦存する場を地熱系と呼ぶ。地熱資源は(資源という文言が付いている以上、人類にとっての利用可能性を含めて考えなければならないから)、熱源だけで構成されるわけではない。地熱資源として必要な構成要素は、「熱源、地熱流体及び、岩石中の孔隙や割れ目」の3つとされる。この3つの構成要素を定量的に表す物理変数として、熱源→温度、 地熱流体の量→圧力(分布)、孔隙→透水係数が、それぞれ用いられる。取り扱い上の理由から(?)、正確には、透水係数は透水係数の常用対数(つまりlog10透水係数)が用いられているが、本稿では、両者を区別せずに用いる🐾8。
地熱系≒地熱貯留層は、以下のように形成される:地表から地下へ浸透した冷たい流体が、孔隙を通じて地下深部へ浸透する。この冷たい流体は、熱源で加熱される。冷たい流体と熱い流体(地熱流体)との密度差等が駆動力となり、地熱流体は、孔隙を通じて地表へ向かって上昇する。ただし、上昇するものの、あるところで留まるから、貯留層が形成される。地熱流体の上昇が、キャップ・ロック(日本語では、帽岩)と呼ばれる孔隙が少ない”岩石状の地層”によって留められることで、地熱貯留層が形成される。なお、地熱貯留層の構造をモデル化することを、地熱系概念モデルを構築する、と表現する。
本論文では、岩手県岩手郡雫石町にある葛根田(かっこんだ)地熱地域を取り扱っている。葛根田地熱発電所は、昭和53年5月に1号機が稼働している。
🐾8 本論文では、permeabilityが使われているが、透水係数(hydraulic conductivity)と浸透率(permeability)も区別しない。細かく言うと、透水係数と浸透率は、物理変数として異なる(次元があ異なる。透水係数=[LT-1]、浸透率=[L2])。流体として水だけを扱う場合、透水係数が使われるらしい。原油などを含めたより一般的あるいは多相流体の場合、浸透率が使われるらしい。
(1) 地熱開発における物理について
地熱資源の3つの構成要素を定量的に表す物理変数は、「温度、 圧力、透水係数」であった。地熱貯留層から取得される観測データを使って、この3変数を推定することが、地熱系の逆問題解析である。地熱系の逆問題解析は、熱流体解析における逆問題という形で定式化される。これはマルチフィジクス問題であり、熱と流体流動を記述する式が、連成している問題である。当該問題をシミュレートすることを、地熱開発の文脈では、自然状態シミュレーション❚補足❚と呼ぶ。
熱流動は、エネルギー保存則という形式でPINNsに組み込まれる。熱伝導と熱移流が等しいという関係式が、熱流動を記述する式となる。流体流動は、質量保存則という形式でPINNsに組み込まれる。流体力学の言葉を使うと、連続の式である。つまり、連続の式が、流体流動を記述する式である。また、地熱流体の挙動は、多孔質媒体中の流体流動として記述されるので、流体の速度を求めるためにナヴィエ・ストークス方程式は使用されない。流速は、ダルシー則から導出される。
❚補足❚
地熱開発(地熱発電の開発)において、自然状態シミュレーションは、開発する前(自然状態)の地熱貯留層内に対する「地熱系概念モデル」に基づくシミュレーションで、「地熱資源量評価フェーズ」で実行される。自然状態シミュレーションと現地観測データ(を使ったキャリブレーション)に基づいて、「自然状態モデル」が作られる。自然状態モデルを基に、生産予測シミュレーションが実行され、地熱発電可能量が推定される。
本論文の内容は、自然状態シミュレーションをPINNsで行う、という研究である。
(2) ネットワーク・アーキテクチャ等について
PINNsモデルとして、3つの全結合ニューラルネット・ワークを使用した。1つのネットワークは4つの隠れ層と50ノード/層を持つ。各ニューラルネットワークは、座標を入力として、温度、圧力、または透水係数、のいずれかを出力する。温度、圧力、および透水係数の出力値は、PDE損失(物理則損失☞【3】(1)1⃣)と境界損失(☞【3】(1)1⃣)を計算するために使用される。
活性化関数として、双曲正接関数を使用する。ネットワーク・パラメータの初期化には、(比較的一般的な)Xavier スキームが使用されている。
【3】本論文の技術的要素
(0) 地熱系逆問題解析とPINNsとの相性が良い理由
従来の数値シミュレーションとは異なりPINNsは、必ずしもすべての物理法則と境界条件を必要としない。そのため、シミュレーションに必要なすべての条件が揃っていない場合でも、PINNsを適用できる。本論文の場合3次元(というタフな)問題を扱っているので、境界条件の設定もタフになる(☞下記(1)0⃣参照)。具体的には、PINNsには次のような利点があるため、地熱系逆問題解析とPINNsとは相性が良いと考えられる。
数値計算において質量流速を含めずに計算を実行することは不可能であるが、PINNはすべての境界条件を指定せずに学習させることができる。この特性を利用し、本論文では底面境界条件としてノイマン境界を設定する際に、質量流速を指定しなかった。
(1) 損失関数
0⃣ 境界損失・境界条件
本論文は、3次元問題に取り組んでいるため、境界条件の取り扱いが煩雑になる。上面境界には、一定温度・圧力(ディリクレ条件)が使用された。側面境界条件の設定は、現実的な条件に適合しないため、本論文では側面境界条件を考慮しない。実際には、側面境界条件と底面境界条件には多くの不確実性があるため、境界を設定せずに計算することが望ましい場合がある。
底面境界条件は不確実ではあるものの、深度予測性能を向上させる上で重要であるため、本論文では、一定熱流(ノイマン条件)と一定温度・圧力(ディリクレ条件)の両方が設定された。ノイマン条件を用いた場合、境界損失における重みは動的に調整される。ディリクレ条件を用いた場合は、重みは固定値である。
底面境界条件は、ディリクレ条件でもノイマン条件でも、止むを得ず、既知の一定値として設定されている🐾9。しかし実際には、予測誤差を減らす上で底部境界条件の精緻化が重要であることが、本論文では示されている。
🐾9 ノイマン条件は、熱流束で与えている。熱流束は、葛根田地熱地域周辺の温度と熱伝導率の測定値から推定できる。熱伝導率は、0.60W/(m・K)が用いられた。ディリクレ条件を与える底面の温度と圧力は、利用可能な温度ログの空間外挿によって近似されると仮定された。
1⃣ メイン
本論文は逆問題を扱っているので、損失関数は以下の形を取っている:
総損失関数=データ損失+PDE損失+境界損失🐾10
PDE損失=重み1×質量保存則損失+重み2×エネルギー保存則損失🐾11
境界損失=1.0×上面境界損失+重み3×底面境界損失
データ損失のローカル重みは標準的な、1/データ数である。データ損失のグローバル重みは、1.0と考えられる。PDE損失は、ローカル重み×グローバル重みが、重み1及び重み2と見做せる。境界損失も、ローカル重み×グローバル重みが、1.0と重み3と見做せる。重み1~3は、動的に調整される(☞下記(3)を参照)。
🐾10 本論文で使われている文言を使うと、総損失関数=Misfit(データ・ミスフィット損失)+Physics(物理則損失)+Bounds(境界損失)である。
🐾11 本論文で使われている文言を使うと、質量保存則損失=Mass Balance、エネルギー保存則損失=Energy Balanceである。質量保存則は、字面通り。エネルギー保存則は、移流による熱の移動量と、伝導による熱の移動量が等しくなることを示す。
(2) 学習戦略
1⃣ 基本戦略
最適化アルゴリズム(オプティマイザー)として、標準的なAdam を使用した。ネットワークの学習は、まず、データ損失項に対して15,000 エポック実行され、次に全ての損失項に対して30,000 エポック実行された。最初にデータ損失項のみで学習し、次にすべての損失項で学習する理由は、ネットワークの学習効率が向上するためである。
学習率は、5 × 10−3から5 × 10−5まで動的に調整した。
2⃣ 損失をさらに減らすための試行
損失をさらに減らすため、(PINNsにおける教科書的な推奨最適化アルゴリズムの一つである)Adam+L-BFGSが試されている。具体的には、Adamで30,000エポック学習した後、L-BFGSが収束するまで使用された。L-BFGSの使用により、検証損失が減少したケースもあったが、収束基準を満たすことができないケースもあった。本論文は、オプティマイザーはAdamで十分と結論している。
(3) 係数アニーリング:ローカル重み×グローバル重みの更新方法
1⃣ 計算式
本論文では、以下のような重みの更新方法を、係数アニーリングと呼んでいる。PDE損失の重み1及び重み2、並びに境界損失の重み3は、次のように更新される。更新頻度は、100エポックごとである。
あるエポックにおける重み=(1ーα)×1つ前のエポックの重み+α×係数
ここで、α=0.4と設定されている。また、”係数”は、|勾配|の平均値/|勾配|の最大値、で計算される。以下は為念・・・勾配とは、PDE損失項並びに境界損失項の勾配である。|・|は絶対値をとることを表している。平均値及び最大値はエポック毎に計算される。
2⃣ 遡って、背景
係数アニーリングを採用した背景は、以下の通りである:勾配の大きい損失項はネットワーク・パラメータ更新に反映される可能性が高い一方、勾配の小さい損失項は更新に反映される可能性が低くなる。さらに、各損失項の勾配はエポック毎に異なるが、勾配変化はエポック毎に似ていた。つまり、係数アニーリングを採用することで、損失項の違いとエポックの違いがパラメータ更新に与える影響を吸収して、全ての損失項の影響を、各エポックにおいて均等に反映させることを目指している。
3⃣ 残念な定量的結果と、強調すべき定性的結果
ただし、「この係数アニーリングを用いたPINNsによる解析領域全体の温度、圧力、および透水係数の予測値の平均誤差は、定数係数を用いたPINNsによる予測値と同程度であった」。
その一方で、係数アニーリングを用いることで、物理的解釈性は向上したと、本論文は主張する。質量保存則損失及びエネルギー保存則損失の誤差が低減したことを理由として上げている。係数アニーリングを用いた場合、質量保存則損失量とエネルギー保存則損失量は、約1/10に減少した。この事実は、PINNsが正しい物理モデルを学習したことを示している、と言いたいのであろう。
(4)追加の損失項を考慮する
0⃣ 背景
都合上先走って伝えると、温度と圧力(分布)の予測精度においては、PINNsはベースラインを上回ったが、透水係数に関しては、ベースラインと同程度であった。そこで、新たな施策が実行された。その一つが、損失関数に新たな損失項を追加することであり、もう一つが転移学習(☞下記(5)参照)である。
1⃣ マグネトテルリック(MT)損失項
Magnetotelluric(マグネトテルリック:地磁気地電流、MT)法は、地表における自然電磁場の観測を通じて、地球の地下電気抵抗率を調査する地球物理学的手法である。マグネトテルリック(MT)データ(の観測値と予測値の差異)で構成されるMT損失項を損失関数に、そのまま追加すると、損失関数の収束が非現実的に遅くなった。さらに、温度、圧力、および透水係数はすべて電気抵抗率の影響を受ける。この相互相関により、ネットワーク学習が進まない可能性があるという懸念が生じる。そこで、”温度、圧力、および透水係数”の中で、透水係数が電気抵抗率に最も敏感であることに着目し、MT データを使用して透水係数を更新するようにネットワークを学習した。
2⃣ 結果
MT損失項を追加した結果、深度-1,200m未満の浅層貯留層で予測精度の向上が確認されたが、その他の領域では、予測精度の向上は見られなかった。定量的に言うと、観測値と予測値との誤差が0.45から-0.21に(絶対値で言えば)小さくなった。なお、透水係数は、常用対数で表されていることに注意。
3⃣ 予測精度の向上が限定的である理由
感度分析の結果、中高比抵抗帯における透水係数の誤差は、MTデータに対してそれほど敏感ではないことが示された。本論文における浅層貯留層は、低比抵抗帯であった(ため、予測精度の向上が確認されたと考えられる)。地熱貯留層は(地熱流体が天水(=雨水)起源と仮定されるので)、一般的に低比抵抗から中程度の比抵抗を有する。このため、(本論文のケースに限定されず)一般的なケースでも、地熱貯留層はMTデータに対して良好な感度を示すこと、つまり、MTデータが地熱貯留層内の透水性分布の精緻化に有用である可能性がある。
(5) 転移学習
まず、PINNsに透水係数の(有限差分法よる)数値モデルを事前学習させる。次に、転移学習を用いて、坑井データでモデルを再学習させる。この転移学習フレームワークは、透水係数の精度向上には有効であった。その一方、転移学習戦略を使用した場合、温度と圧力の予測誤差はわずかに増加した。この理由を、本論文では、「自動微分と有限差分法による勾配計算の精度に差があったため」と推測している。
(6) 適切な勾配計算の検証
勾配計算は、深層学習モデルにおいてキモである。それは、当然PINNsにも当てはまる。本論文は、「自動微分(AD)の実装が不適切であれば、正確な勾配計算はできない」という先行研究における指摘を受けて、ADを使って算出された勾配の精度を検証している。具体的には、先行研究に基づいてADと有限差分法(FD)で計算された温度勾配と圧力勾配の差異を調べている。ADが適切に実装されていれば、ADとFDの勾配の差は、特徴的な誤差パターンを示す(らしい)。
結論を述べると、本論文で実装されたADは、勾配を正確に計算していることが確認された(ので、PINNsの出力は精確であることが期待できる)。実際PINNsによって、葛根田における地熱貯留層の全体的な空間パターン及び特徴的な温度層の構造🐾12が、正しく予測されたことが示されている。
🐾12 温度に関して2層構造を示す。それぞれ高透水性層である浅層貯留層と、低透水性層である深層貯留層が対応する。浅層貯留層は深度約1,500m迄で、温度は200℃程度。深度約1,500m以降が深層貯留層で、温度は250~350℃。
【4】比較結果
(0) セットアップ
0⃣ ハードウェア環境
32コア32スレッド、最大クロック速度2.5GHzのAMD EPYC 7502P CPUを搭載したワークステーションを使用した。アクセラレーションに使用したGPUは、NVIDIA RTX A6000であった。システムは、3.2GHzで動作する256GBのDDR4メモリを搭載。ストレージは、キオクシアCM6-RシリーズのSSDを採用した。
1⃣ データセット等
予測精度に対する井戸数の影響を調べるため、10、15、30 本の垂直井戸を考えた。各シナリオで、参照モデルの格子位置から5つの異なる井戸位置をランダムに選択した。ネットワークの学習では、標高が-1,600m以下のこれらの井戸のデータを学習データとして使用し、それより深い井戸のデータは、検証データとして使用した。学習データ・ポイントの数は、井戸数が 10、15、30 本のケースでそれぞれ 130、195、390 であった。
葛根田参照モデルのデータが存在する 18 × 11 × 18 ポイントについて、予測値と葛根田参照モデルのデータとの差の絶対値を計算し、その平均(=”平均絶対誤差”)を予測モデルの全体的な予測誤差とみなした。
2⃣ ベースライン・モデル
深層ニューラルネットワーク(DNN)、クリギング法(KRG)、XGBoostの3つがベースライン・モデルである。深層ニューラルネットワークとは相当曖昧な表現であるが、PINNsの損失関数において、PDE損失と境界損失を取り除いたもの、という認識で良い。
KRG は、単なる空間補間法に過ぎない🐾13。これを、ベースライン・モデルに含めて良いのかという疑問が生じる。KRGを適用する際、まず坑井データを深度方向に線形外挿する。次に、坑井データを深度方向にスライスし、各深度についてKRGを用いて水平2次元データを補間する。
🐾13 対象空間に対して、確率場を用いて共分散から確率的に補間を行うことで、データの空間的分散性を考慮した補間が実行される。
(1) 平均絶対誤差の比較結果
1⃣ 温度
PINNsの誤差が最も小さい(およそ20℃程度)。KRGの誤差が最も大きく(50℃程度)、XGBoost(40℃程度)、DNN(30℃程度)の順番で精度が上がる。
2⃣ 圧力
PINNsの誤差が最も小さい(およそ100kPa程度)。XGBoostの誤差が最も大きく(およそ600kPa程度)、KRG(180kPa程度)、DNN(150kPa程度)という順番。
3⃣ 透水係数
既述通り、PINNsと他モデルの誤差は同程度。正確には、XGBoostの誤差が最も小さい(およそ0.9m2程度)。PINNs、DNN、KRGはおよそ1m2程度。
予測精度の改善については、【3】(4)2⃣を参照。
(2) 為参考:学習時間のまとめ
1⃣ Adamのみ
PINNsの学習時間は、(5回実行で)平均約48.5時間かかった。坑井数によって計算時間に大きな変化はなかった。
2⃣ Adam+L-BFGS
平均 77.0 時間を要した。
3⃣ MT項を考慮
平均 81.3時間を要した。
【5】制限及び注意点のまとめ
(1) 制限
1⃣ 不確実性の定量化
本論文では、PINNsの予測における不確実性は定量化されていない。坑井の配置と空間密度によっては、PINNsは観測値に大きな感度を持たない局所的な透水係数構造を予測できない可能性がある。さらに、自然状態の地熱モデリングの非一意性により、物理量を正確に予測できない領域が必然的に存在する(らしい)。したがって、PINNsの予測における不確実性の定量化は、予測に基づいて意思決定を解釈および実施するのに役立つと考えられる。
2⃣ 計算コスト
PINNsの利点の1つは、ネットワークを一度学習すると予測が高速になることだが、リアルタイムの学習と予測が必要な場合は、学習の計算コストを削減する必要がある。解決策としては、モデル分解や分散学習などの並列化手法が挙げられる。
3⃣ データ入手性
地殻の透水性を直接測定するには、無傷のコアサンプルを入手する必要がある。しかし、地熱地域では十分なコアサンプルが得られないことが多く、坑井沿いの透水性測定は一般的に疎らである。坑井沿いの透水性測定が疎らであれば、PINNによる予測誤差が増大する可能性がある。解決策としては、坑井検層による透水性推定が挙げられる。
(2) 注意点
1⃣ マルチスケール特性
地熱地域は一般的に不均質な破砕岩で構成されており、マルチスケール特性とスケール依存の岩石特性を持つ。このマルチスケール特性のため、坑井から得られた岩石特性が現場スケール特性と一致するかどうかを慎重に確認する必要がある。
2⃣ 相互整合性の検証
本論文で行われたように、坑井データとMTデータを統合してモデリングを行う場合、データが相互に整合していることを確認するための品質チェックを行うことが不可欠となる。
【6】考察
(0) 地熱系3次元逆モデリングにPINNsを適用したら、透水係数の予測だけ性能が低かったので、透水係数の予測誤差も減らす方法を考えました、という内容。
(1) 諸々の理由により、近時の地熱開発は、超臨界地熱を活用するという方向で行われていると思われる。超臨界地熱とは、超臨界状態(あるいは、それに準じる状態)にある地熱流体の地熱である。「超臨界状態=より高温・高圧の状態」なので、より大きな発電量が期待できる。また、超臨界地熱貯留層は、(従来型の地熱貯留層)より深部に存在するため、温泉への影響も少ない(業者への説得が比較的容易)とされる。超臨界地熱の地熱流体は、海水起源とされる。そうであれば、比抵抗は高くなる可能性があると思われる。
つまり、トレンディー(!)な超臨界地熱開発では、MT損失項を追加することによる透水係数の予測精度向上が、期待できない可能性があると思われる。仮にそうであれば、MT損失項の議論は、あまり意味がないことになる。
(2) 地熱開発×PINNsというセットアップは、厳しい言い方をすると、地熱発電可能量の推定に使えてナンボの世界であろう。その意味では、不確実性定量化(☞【5】(1)1⃣)が欠かせないだろう。PINNsをベースとするのであれば、ベイジアンPINNsで対応する、ということになるだろうか。
チリのマヨール大学・米ハーバード大学他の研究者は、「PINNsは量子最適制御において、優れた性能を発揮する」と主張する論文(以下、本論文[*89])を発表した(23年12月7日@arXiv)。最適制御にニューラルネットワークを適用するというアプローチは、古典の範疇でも比較的新しい。
本論文では、量子コンピュータへの適用を念頭に、量子最適制御を議論している(ことが本論文のSUPPLEMENTAL MATERIALを見ると、分かる)。
【1】本論文の主張
本論文は、少数自由度の開放量子系を対象とした、PINNsによる量子最適制御は、以下の通りである主張する。
(1) 量子状態の遷移(分布の移動)を、低エネルギー消費、短時間、かつ高忠実度で達成する。
(2) 学習パラメーターが変更された場合に堅牢であり、標準的な方法と比較してより良い結果を提供する。
【2】事前整理
(0) 最適制御とは何か?
本論文は、最適量子制御を扱った論文である。最適量子制御は、最適制御の量子版という意味になる。それでは、最適制御とは何か。最適制御(問題)をより一般的に定義すると、「制御目的を表す量を最小にするような制御入力(操作量)を求める」問題となる [*90]。工学的に具体的な制御目的を表す量には、時間や距離、エネルギー消費量などがある。やや狭く定義すると、「初期状態と目的状態が与えられた時、初期状態を目的状態に駆動する制御外場(制御入力)を設計する」問題となる。量子系において、このような制御外場の存在は、特定条件下で保証されているようである[*91]。
制御入力に対する最適性条件は、多くの場合、手計算では解けない(解析解を求めることが、一般的には不可能)。さらに、計算コストから数値計算でも難しいと考えられてきた。そうなると、機械学習・深層学習の出番となる。ただ、最適制御問題に深層学習を適用するというアプローチは、古典の範疇でも、まだ新しいようである(例えば、2021年11月の研究[*92])。
💡 ちなみに、「微分方程式を制約条件とする最適化は、最適制御理論の主題」である、という身も蓋もない?主張からスタートすると、「最適制御問題が、PINNs向きである」ことが肚に落ちる。
(1) そもそも論-本論文でPINNsは、何をやっているのか
本論文が、何をやっているかを、以下説明する。本論文における量子制御とは・・・を説明する前に、まずは、概要を掴もう。そのために、自然に存在している量子系を人工の量子系で模して、人工的に制御することを考えよう。例えば、人工原子で量子ビットを作成し、量子ビットを制御して量子計算を行うこと(量子コンピュータ)をイメージすると、分かり易いだろう。その場合、レーザー光やマイクロ波パルスを照射して、量子ビットを制御する。PINNs寄りの言葉を使うと、量子ビットを所望の状態に変化させるパラメータ((0)で現れた文言を使うと、制御入力)を見つけることが、本論文におけるPINNsの目的である。
さらに言うと、本論文の問題設定は、逆問題(かつ外挿問題)に相当する。そして蛇足ながら、初期値問題ではあるが、境界値問題ではない。
(2) 本論文における量子制御とは・・・
詳しい内容を把握するため、量子物理に戻ろう。唐突だが、本論文が扱う対象は、少数自由度の弱結合開放量子系である。この設定のお陰で、密度演算子の時間発展は、微分方程式(量子マスター方程式)で記述可能となる。少数自由度として本論文では、具体的には、2準位系~4準位系が登場する。
本論文における量子制御とは、基底状態|g⟩と励起状態|e⟩の量子遷移を制御する、という意味である。これを制御系dx(t)/dt=A・x(t)として見た場合、状態変数(ベクトル)x(t)は、密度演算子と|g⟩及び|e⟩から構成できる。有体に言えば、x(t)は、密度行列の要素ρij=⟨i|ρ(t)|j⟩である。ここで、|i⟩は、|g⟩もしくは|e⟩である。密度行列の対角要素ρiiは、|i⟩から|i⟩の遷移確率(つまり、|i⟩に留まる確率)を表し、非対角要素ρijは、|i⟩と|j⟩の位相関係(コヒーレンス)を表す。ダイナミクスを記述する行列Aの行列要素は、パラメータ(制御理論の文脈では、制御パラメータあるいは制御変数と呼ばれる)を含んでいる。
密度演算子は適当な初期値を与えると、 量子マスター方程式の解として得られる。深層学習・ニューラルネットワーク(NN)寄りの表現を使うと、本論文では状態変数x(t)は、量子マスター方程式を介して密度演算子から「生成される」。従って、本論文のNN(正確には、PINNs)は、データ・フリーで学習される。dx(t)/dtは、(Pytorchパッケージの)自動微分を使って計算される。
(3) 損失関数
本論文における損失関数Lは、次のように4つの項の和で表される。L=Lmodel+Lcontrol+Lconst+Lreg。一般的なPINNsの文脈で言うと、LmodelはPDE損失で、Lcontrolは、データ損失である。Lconstは、支配方程式とは異なる物理法則に関する(ソフト)制約に関する項目である。流体解析を例にとると、連続の式(質量保存則)を満たすように構成した損失関数が該当する。本論文では、4準位系の取り扱いにおいて、登場する。最後のLregは、正則化項である。
逆問題なので、データ損失に相当するLcontrolが含まれている。なお、初期損失は(デフォルトでは)ハード制約のため、最適化計算には含まれていない。補足情報で、ソフト制約とした場合との比較がなされている†1。
†1 初期損失Licを追加した損失関数をL’とする:L’=L+λLic。λが小さい(λ=1)の場合は、ハード制約(つまり損失関数がL)とソフト制約(つまり損失関数がL’)に対する「制御入力と量子忠実度の時間挙動、ダイナミクス」に関して、違いがほぼない。ただし、λを大きくすると、L’の収束性が低下する。
【3】本論文で行っていること
(0) 前捌き
少数自由度の弱結合開放量子系を扱っている本論文では、2準位系、3準位系、4準位系に対して、量子最適制御を適用している。ただし、2準位系は定性的に取り扱われているに過ぎない。4準位系は、本文では一言触れられているだけである(SUPPLEMENTAL MATERIALで、定性的に取り扱われている)。定量的に取り扱われているのは、3準位系のみである。
(1) 2準位系のセットアップ
2準位系は、基底状態|g⟩と励起状態|e⟩があり、|e⟩に制御入力(制御外場)を作用させる制御系として設定されている。|g⟩は、電磁波を吸収して|e⟩に遷移する。|e⟩は、電磁波を放出して|g⟩に遷移する。適当な初期(定常)状態、目的(定常)状態、及び物理パラメータを設定し、解析的に最適化された結果とPINNsを使って最適化された結果を比べて、後者が優れているとする。優れているの意味が明示されていないが、合理的に推測すると、目的定常状態に達するまでの時間が、より短いという意味であろう。
具体的な初期(定常)状態は、0.2775 |e⟩⟨e| + 0.7225|g⟩⟨g| + [(−0.1106 + i0.0083)|g⟩⟨e| + c.c.]、目的(定常)状態は、(1/2)(|e⟩⟨e|+|g⟩⟨g|)とされている(c.c.は複素共役)。PINNsの結果は、忠実度0.99である。
(2) 3準位系のセットアップ
1⃣ 概要
3準位系の例は、2準位系の例と異なり、具体的でイメージし易い。3準位系の制御目的は、損失のある中間状態|3⟩を介して、初期状態|1⟩から、目的状態 |2⟩に分布(原語ではpopulation)を効率的に移動するための、最適な制御外場Ωp(t)およびΩs(t)を見つけることである(標準的な最適制御問題の設定)。Ωp(t)とΩs(t)は、制御外場のラビ周波数であるが、制御外場のラベルとしても使用している。
Ωp(t)は|1⟩⇆|3⟩に、Ωs(t)は|3⟩⇆|2⟩に携わる。下付き添え字pはポンプ光を、添え字sはストークス光を意味している。また、Ωp(t)及びΩs(t)は、<10と制限されている。
2⃣ 制御目標
制御目標 は、㊀|3⟩の分布を最小にすること、㊁エネルギー消費量(制御外場の作用)を最小化すること、である。㊀の定量化は、p2=Tr[ρσ22]で行われている。つまり22=|2⟩⟨2|の期待値である。|1⟩から|2⟩への分布移動において、中間状態|3⟩の残存を最小化することは、忠実度が高い(高忠実度)、と表現されている。
㊁の定量化は、Ā=∫(|Ωp(t)|2+|Ωs(t)|2)1/2dtで行う(注:本論文で使われてる記号はĀ ではない)。Āは、tについて、0から分布の移動時間tfまで積分する。tfは、最も高い確率の目的状態に到達するのに必要な時間として定義される。
3⃣ 他の制御手段との比較
❶PINNsは、4つの他制御手段(❷STIRAP†2、❸STIREP†3、❹インバース・エンジニアリング†4、❺MOD-SATD†5)と比較されている。
㊀は、❶0.97、❷0.98、❸0.98、❹0.97、❺0.98である。㊁は、❶7.3❷128.6、❸53.3、❹19.8、❺50.0である。分布の移動時間tfは、❶2.0、❷35.0、❸9.4、❹3.0、❺13.0である(単位は、任意単位a.u.)。なお、 Ā/tfは、❶3.65、❷3.67、❸5.67、❹6.60、❺3.57である。
4⃣ 評価
PINNsによる制御は、㊀において特に優れていないが、㊁において優れている。これは主に、tfの短さがもたらしているものと考えられる。
また、PINNsが学習パラメータの変更に堅牢であるとされている。これは2光子による離調(detuning)δが、STIRAPには悪影響を及ぼす(δが増加するとSTIRAPが劣化する)一方で、PINNsによる制御には悪影響を及ぼさないことを意味しているようである。またδ≠0の場合の、他の制御手段の最適化は自明ではないそうである。
まとめると、本論文では、次のように主張されている:PINNSは㈠低エネルギー消費かつ短時間で、高い忠実度を達成する。㈡学習パラメーターが変更された場合に堅牢であり、標準的な方法と比較してより良い結果を提供する。
†2 誘導ラマン断熱過程(STImulated Raman Adiabatic Passage)。STIRAPは断熱時間発展に従うので、遅い。STIREP、インバース・エンジニアリング、MOD-SATDは、全て時間を短縮するための改善を施した代替手法、と考えてよい。なお、SUPPLEMENTAL MATERIALには、断熱ショートカットを使って高速化したSTIRAPも取り上げられている。
†3 誘導ラマンexact過程(STImulated Raman Exact Passage)。インバース・エンジニアリングの手法を取り込むことで高速化を計っているらしい。
†4 時間依存の補助パラメータを”上手く”導入するところがミソらしい。Ωp(t)とΩs(t)は、補助パラメータを使って表現される。補助パラメータを求める方が速ければ、結果的に、より速くΩp(t)とΩs(t)を見つけることができる。
†5 断熱性による損失の影響を打ち消しながら、断熱条件を回避する、別の代替手段らしい。
(3) 4準位系のセットアップ
4 準位系には、より多くの非線形方程式が含まれており、新しく追加された状態へのクロストークの可能性が含まれる。つまり、4 準位系への拡張は簡単ではない。4 準位系に対する本論文の主張は、「PINNsがネットワーク・アーキテクチャを変更せずに 4準位系を処理できる」である。具体的には、損失関数に、新しい項 Lconstを追加するだけである。
4準位系の制御目標は、⓵損失のある中間状態(|3⟩)の分布を最小化し、⓶エネルギー消費を最小化し、⓷状態|4⟩ へのクロストークを最小限に抑えて、状態|1⟩から状態|2⟩ への分布移動に成功する PINN を学習することである。⓷は選択性を保証するものであり、3準位系には必要ない。
PINNsによる制御の結果、適当な定常状態に到達することが、(図11)に示されている。
(4) ハイパーパラメータ等†6
オプティマイザー・・・Adam
活性化関数・・・正弦関数(sin)
隠れ層の数・・・4、5、5
エポック数・・・4、2、2(全て、×104)
ニューロン数・・・200、150、150
学習率・・・0.1、8.0、8.0(全て、×10-3)
η†7・・・0.1†8、0.2、0.2
χ†9・・・1.0、2.8、2.8(全て、×10-3)
†6 3つの数値が記載されている場合は、順番に、2準位系、3準位系、4準位系に対する数値である。
†7 Lcontrol(データ損失)にかかる重みである。
†8 SUPPLEMENTAL MATERIALの表Ⅱでは0.1。本文図3では1となっているが、0.1の誤植と思われる(0.1の方が、整合的である)。
†9 Lreg(正則化項)にかかる重みである。
【4】考察
(1) (量子、古典は別として)最適制御は難しい。なぜPINNsで上手く行ったのか。仮に、「最適制御問題は、ニューラルネットワークから見ると、単に逆問題(かつ外挿問題)に過ぎない」と整理できれば、PINNsで上手く言っても不思議ではない。この仮に・・・を是とすれば、(古典)最適制御でもPINNsは有効に機能するはずである➡ 人工衛星の軌道推定に関する論文[*85](こちらを参照)は、PINNsを(古典)最適制御に適用した論文と見做すことができるかもしれない。もちろん、[*85]でPINNsは有効に機能している。
(2) もちろん「PINNsは、最適制御問題を簡単に解ける!」は安直過ぎる。そんなことはないだろう。PINNsの学習は、実は難しい(と言われている)。本論文でなぜ上手く言っていったのか、をテクニカルに考えると、以下のことが言えるかもしれない。
1⃣ 損失関数に多数の項目を詰め込めるから。実際、4準位系では、第二のPDE損失(項)と考えられるLconstを導入することで、安定的な学習ができた、としている。
2⃣ 他事例では、ほぼ現れない正則化項が導入されている。
3⃣ 量子マスター方程式の解を使ってPINNs学習を進めるから、自然に、初期値を与える点から徐々にコロケーション点が拡大するという流れになっている(そもそも、初期値問題ではあるが境界値問題ではないので、コロケーション点の構成に(再)サンプリングを用いるというアプローチは、ない)。コロケーション点を規律に従って徐々に増やすという手法は、別稿で示した通り、安定性には寄与するはずである。
(3) 正則化項含めて、損失関数の重みは、試行錯誤的に決めるしかない(コロケーション点の数が与えられるわけではないから)。試行錯誤的に決定するのは、面倒だったろうが、量子コンピュータ(量子ビット)の制御なら十分ペイするのだろう(リアルタイム制御が可能かは分からないが・・・)。
(4) 学習パラメータの変更に対する堅牢性は、量子コンピュータへの応用を見据えた上で、貴重な特徴と言えるだろう。
比較的単純で標準的な問題に対しては、量子化されたPINNs(QINNs)は(古典的な)PINNsよりも、精度やパラメータ効率が向上する可能性がある。一方、「高次元、非定常、非線形システム」におけるQPINNsのパフォーマンスについては、ほとんど未解明のままである。斯様な問題意識の下で、以下に示す研究が行われた。イスラエル工科大学の研究者は、「QPINNsは、ハイリスク・ハイリターン」と解釈することが可能な論文(以下、本論文[*123])を発表した(25年6月29日@arXiv)。
本論文を機械的に要約すると恐らく、「QPINNsは、PINNsよりもパラメータ効率が高い」というステートメントが、生成されるであろう。もちろん、そのステートメントは本論文の主張を正しく反映しているものの、そのステートメントだけでは、やや本質を外しているような気がする(☛【5】(1))。
【1】本論文の主張
本論文は、「特定のセットアップ」におけるQPINNsに対して、以下を主張する:
(0) 特定のセットアップとは、具体的には、2種類の媒体における2次元電磁波伝播問題である。媒体は、自由空間(真空)と誘電媒体の2種類である。便宜上、真空中の伝播問題をセットアップ1、誘電媒体中の伝播問題をセットアップ2とする。
(1) セットアップ1➡ 新たな学習障害が発見された。本論文では、ブラックホール崩壊、と呼ばれている(☞【3】(0))。
(2) セットアップ1➡ (1)の学習障害は、新たな損失項を損失関数に加えることで、回避できる。(☞【3】(1)1⃣㈡)
(3) セットアップ1及び2➡ 少ない数の学習可能パラメーターを使用しながら、古典PINNsベースラインと同等の精度を達成する(☞【4】(3)1⃣㈠)。
(4) セットアップ1及び2➡ QPINNsはPINNsよりも速くPDE解を学習した。(☞【4】(3)1⃣㈡)。
【2】事前整理
(1) 電磁場のエネルギー保存則
電磁場のエネルギー保存則は、ポインティング🐾1ベクトルSと電磁場のエネルギー密度u、電流密度ベクトルJ、電場ベクトルEを使って、
-∂u/∂t=∇・S+J・E
と表される。・は内積。ポインティング・ベクトルSは、S=E×Hである。Hは磁場ベクトル。EもHもベクトルなので、×は外積。なお、本論文では、J=0と設定されている。
🐾1 人名(ジョン・ヘンリー・ポインティング)。ポインティング のスペルは、Poynting。
【3】本論文の技術的要素
(0) ブラックホール崩壊
本論文は、「近似PDE解に向かって数百エポック降下した後、突然自明解に降下する、という新しい現象:ブラックホール(BH)崩壊を観測した」とする。このBH崩壊により、解は物理的な意味を持たなくなり、t=0を除くあらゆる空間および時間点で、その値はほぼ0(自明解)になる。この自明解は、初期条件のみを満たすという特徴を持つ。
BH崩壊は、以下に述べる理由から、不毛な台地(BP)等の学習障害とは異なると、本論文では判断している:高エンタングルメント状態や、非局所コスト関数と関連付けられることが多いBPとは異なり、BHはエンタングルメント指標と明確な相関を示さない。さらに、局所コスト関数を使用しているにもかかわらず、BHは出現する。さらに、BP等は通常、最適化の開始から勾配が消失する形で現れるのに対し、BHは『初期の学習が成功した後にのみ』発生する。
(1) 損失関数
0⃣ 概要ー頭出しのみ
総損失関数=PDE損失+初期条件損失+対称性損失+エネルギー保存則損失
境界条件損失は、陽的には考慮されない(☞詳細は、(2)3⃣を参照)。
1⃣ 概要の補足
㈠ 対称性損失
ここで言う対称性は、(ゲージ対称性のような)難しい対称性ではなく、鏡映対称性を指している。電場、磁場のそれぞれに対して、鏡映対称なPINNs解が出力されても、それは物理的には意味がない解だから、ペナルティを与えるという損失項である。
㈡ エネルギー保存則損失
(損失のない媒体における)マクスウェル方程式の重要な物理的特性は、電磁エネルギーの保存である。周期的境界があり電磁波の吸収がない閉領域で、場の全エネルギーは、時間に対して一定でなければならない。PINNs解は近似誤差のために、この保存則に違反する可能性がある。PINNsに、電磁場のエネルギー保存則(☞【2】(1))強制するために、エネルギー保存項損失が導入される。なお、この損失項の導入は、BH崩壊(☞(0))を回避するために、重要である。
㈢ 為念:初期条件
電場は2次元ガウス・パルス、磁場はゼロに初期化される。
2⃣ ローカル重み
コロケーション点の数の逆数が、設定されている。PDE損失の場合、1/643。初期条件損失の場合、1/642。対称性損失のローカル重みは、PDE損失と同じ。エネルギー保存則損失のローカル重みは1。
3⃣ グローバル重み
PDE損失のグローバル重みが1、その他が10。
(2) PINNs学習におけるその他の工夫
本論文では、PINNs学習を改善するための工夫も、導入されている。
1⃣ 適応的時間的重み
時間依存PDE を解くときにPINNs は、時間的因果関係に違反する可能性があり、誤った解に収束しやすいことが示されている。適応的時間的重みは、当該問題への対応策である。端的に述べると、時間的因果関係の尊重、である。機械学習寄りに言葉を替えると、時間領域カリキュラム学習であり、ネットワークが最初に、初期時間のダイナミクスを学習する(できる)ようにする。
本論文では、次のように行われている:コロケーション点が5つの時間ビンに分割され、学習開始時に、後続の時間ビンに損失の低い残差重みが割り当てられる。これらの重みは、ネットワークが初期時間のダイナミクスに収束するにつれて、徐々に増加する。この方法により、モデルは初期時間の挙動(≈初期条件)に焦点を当てることができるため、因果関係を尊重しながら解を前方に伝播できる。
2⃣ ランダム・フーリエ特徴量(RFF)
ランダム化された正弦波特徴量を用いて、(x, y, t)を高次元特徴空間に埋め込むマッピング層を適用している。具体的には、入力は(x, y, t) ↦ (cos(Ω[x, y, t]T),sin(Ω[x, y, t]T))と変換される。ここで、Ωは固定されたランダム射影テンソルであり、その要素はガウス分布からサンプリングされ、学習中は一定のままである(つまり、学習可能なパラメータではない)。
この変換により、高周波成分が入力表現に組み込まれ、ネットワークがPDE解のマルチスケール特徴を捉える能力が向上し、PINNsに固有のスペクトルバイアスが軽減される。
3⃣ 厳密な空間周期性の強制
x座標とy座標はそれぞれ、領域の長さに応じてスケーリングされた正弦関数と余弦関数にマッピングされ、周期境界条件を強制する。これにより、明示的な境界損失項が不要になる。
4⃣ 周期的な時間領域マッピング
t座標も正弦関数と余弦関数にマッピングされるが、領域の長さではなく「周期時間の長さ」でスケーリングされる。 周期時間の長さは、ニューラルネットワークに追加された学習パラメーターとして設定される。これは、シミュレーションの長さが1周期を完了するのに十分でないためである。
(3) 為念:自作のライブラリ等
また、本論文では、PyTorchを用いた独自の量子シミュレーション・ライブラリを開発し、PennyLaneのdefault.qubitシミュレータと比較して、50倍以上高速であることを確認した、と主張している。なお、Qiskitでの実行は、PennyLaneのものよりも遅かったらしい。
ちなみに、カスタム・シミュレータでは、メモリ使用量も大幅に改善されたらしい。メモリ・オーバーフローなしで実行できた最大のコロケーション点は、カスタム・シミュレータでは873個であったのに対し、PennyLaneのdefault.qubitでは433個であった。
【4】比較結果・評価結果
(0) セットアップ諸々
0⃣ 物理的な問題設定
物理的な問題設定を改めて整理すると、2次元電磁波伝播問題で、媒質は真空と誘電体の2種類。この場合の基礎方程式は、言わずもがな、2次元時間依存🐾2マックスウェル方程式である。本論文における2次元とは、電場がz方向のみ、磁場がxとy方向のみ、であることを指している。
🐾2 通常は、時間依存である(ので、普通の設定)。
1⃣ 古典ネットワーク・アーキテクチャ、ハイパーパラメータ等
古典的なPINNsは、全結合層を備え、4つの隠れ層を持つ。各層は128個のニューロンで構成されているが、RFF(ランダム・フーリエ特徴量、☞【3】(2)2⃣)層直後の層は、RFF層が128個の正弦波出力と128個の余弦波出力を持つため、ニューロン数は256個に設定されている。活性化関数には、tanhを使用した。最適化アルゴリズムにはAdamを使用。学習率は0.001から開始し、2,000エポックごとに0.85倍に減衰した。
2⃣ 量子ネットワーク・アーキテクチャ等
本論文のQPINNsは、古典PINNsの最後から2番目の層をPQC(パラメータ付き量子回路、アンザッツ)に置き換えることで構築された。PQC層は、ネットワークの終端に近い位置に配置されるものの、出力の汎用的な量を保証するため、最後の層には配置しない。
QPINNsは、まず角度埋め込み層を設定し(つまり、量子符号化には、角度符号化が採用された)、次にアンザッツ層、最後にパウリZ測定を設定することで構成される。7量子ビットと4層が使用される。すべてのQPINNsモデルにおける古典的に学習可能パラメータの数は、すべてのアンザッツ・タイプ(後述)で66,848である。なお、アブレーション分析のため、スケーリング変数とアンザッツが複数用意されている(☞(1))。
3⃣ 為念:計算環境等
本論文におけるすべての実験は、古典的GPUベースのノイズなし量子シミュレータ上で実行された。
H/Wは、NVIDIA L40およびA100 GPUを用いた。ミニバッチ処理やマルチGPU学習は使用していない。
(1) スケール変数とアンザッツにかかるアブレーション分析
本論文では、5つのスケール変数と6つのアンザッツに対して、包括的なアブレーションが実施された。
1⃣ 5つのスケール変数:活性化関数出力に対する5つのスケーリング
QPINNsの角度埋め込み層は、活性化層の出力を『スケーリングした』値に対応する角度で、各量子ビットをx軸周りに回転させる。言葉だけだと曖昧かつ分かり辛いので、式を織り交ぜて補足する。活性化関数はtanhであるから、活性化層の出力:y↦tanh(y)に対して、適当な数aを掛けて、まずスケーリングを行う。このスケーリングした活性化層の出力”a×tanh(y)”に対応する角度で、量子ビットをx軸周りに回転させる。
本論文では、5つの異なるスケーリング方法がテストされている。つまり、適当な数aが5種類ある:① a→a、② a→a×π、③ a→(a+1)π/2、④ a→arcsin(a)+π/2、⑤ a→arccos(a)
2⃣ 6種類のアンザッツ
アンザッツは、以下の通りである:❶ハードウェア効率の高いアンザッツ、❷強いエンタングルメント・アンザッツ、❸クロスメッシュ・アンザッツ、➍クロスメッシュ・2回転・アンザッツ、❺クロスメッシュ・CNOTアンザッツ、❻エンタングルメントがないアンザッツ。❷≒❶、➍≒❸、❺≒❸である。
❶及び❷は、広く使われているという理由で選択されている。❶は、1量子ビット回転ゲートとCNOTゲートで構成される。❷は、❶におけるターゲット量子ビットと制御量子ビット間のギャップが増加している。❶及び❷には、84 個の量子学習可能パラメータがある。
❸は、1量子ビット回転ゲートRXと制御RZゲートで構成される。❸を採用した理由は、3つある:1 つ目は、全結合回路が、より接続の少ない回路よりも優れた結果を達成するかどうかを確認すること。2 つ目は、全結合がBHに影響を与えるかどうか、を確認すること。3 つ目は、すべて並列に適用できるハードウェア実装があること。❸は196個の量子学習可能パラメータを持つ。
➍は、❸の1量子ビット回転ゲートRXが、RXRZに置き換わる。➍には、224個の量子学習可能パラメータがある。❺は❸の制御RZゲートが制御NOT(CNOT)ゲートに置き換わる。❺にも、84 個の量子学習可能パラメータがある。
❻は、1量子ビット回転ゲートのみで構成され、2量子ビットゲートは存在しない。このようなアンザッツを使用する動機は、量子機械学習におけるエンタングルメントの役割が十分に明らかではないため、QPINN モデルにおけるエンタングルメントの影響を確認することである。❻にも、84 個の量子学習可能パラメータがある。
古典的な学習可能パラメータの数は、❶~❻共通で66,848である。古典PINNsの学習可能パラメータの数は、82,820である。66,848は、82,820に比べて、19.3%少ない。
(2) 評価指標、グランドトルゥース
評価指標は、電場のz成分EZのL2相対誤差である。グランドトルゥースは、4次パデ近似で計算されたEZ。なお計算は、512×512の空間点と1500時間ステップで実行される。また、計算は5回実行され、平均値と標準偏差が算出された。
(3) 結果
1⃣ セットアップ1:真空の場合
㈠ 学習可能パラメータの数
(古典)PINNsに比べて、QPINNsのL2相対誤差が小さかったスケール変数は、3/5である。2/5はPINNsよりも誤差が大きかった。3/5は、①④⑤である。
アンザッツで言うと、3/6でQPINNsのL2相対誤差が小さかった。具体的には、❶❷❸である。❶~❻共通で、古典的に学習可能なパラメータ数は、PINNsに対してQPINNsが19.3%少ないから、「少数の学習可能パラメーターを使用しながら、古典PINNsと同等の精度を達成する(☞【1】(3))」という表現になっている。量子学習可能パラメータは上乗せされるが、微々たるものである。
㈡ 学習速度
QPINNsはPINNsよりも速くPDE解を学習した。かなり少ないエポック数で、同じレベルの学習損失を達成可能である。正確には、「エネルギー保存則損失項なしPINNs」と「エネルギー保存則損失項ありQPINNs」を比較した結果である。さらに言うと、QPINNsのスケール変数は⑤で、アンザッツは❷である。この⑤で+❷という組み合わせは、セットアップ1のQPINNsにおける最強組み合わせである。目視では、QPINNsは、1万エポック程度少ない(ように見える)。これは相当速く見えるが、指数加速には程遠い。
㈢ エネルギー保存則損失項
セットアップ1の場合、エネルギー保存則損失項がなければ、QPINNsはBH崩壊を起こして、意味のある解を出力できない。エネルギー保存則損失項を考慮することで、QPINNsはPINNs越えを果たす。面白いことに、PINNsは、エネルギー保存則損失項の追加によってパフォーマンスが低下する。
2⃣ セットアップ2:誘電体媒質の場合
㈠ 学習可能パラメータの数
(古典)PINNsに比べて、QPINNsのL2相対誤差が小さかったスケール変数は、1/5である。1/5は、①である。
アンザッツで言うと、ほんの僅かにQPINNSが良いケースは2/6(❸と❻)。PINNsと同じが2/6(➍と❺)。悪いケースは2/6(❶と❷)。ザックリ言って、セットアップ1の結果と正反対に見える。また、1量子ビット回転ゲートだけで(エンタングルメント層がない)❻の精度が高い、という結果も、肚落ちしない。全体的に、信頼性が低いように思われる。
㈡ 学習速度
QPINNsはPINNsよりも速くPDE解を学習した。かなり少ないエポック数で、同じレベルの学習損失を達成可能である。正確には、「エネルギー保存則損失項なしPINNs」と「エネルギー保存則損失項なしQPINNs」を比較した結果である。さらに言うと、QPINNsのスケール変数は④で、アンザッツは❻である。④+❻は、セットアップ2の最強組み合わせというわけではない。目視では、QPINNsは、やはり1万エポック程度少ない(ように見える)。
㈢ エネルギー保存則損失項
セットアップ2ではBH崩壊は発生しないので、 エネルギー保存則損失項は不要である。PINNsの場合と同様に、セットアップ2ではエネルギー保存則損失項を考慮すると、パフォーマンスが落ちる(L2相対誤差が大きくなる)。本論文では、その理由を「PDE損失項の最小化を犠牲にして、エネルギー保存則を満たすように強制している可能性がある」と推測している。
【5】考察
(0) 量子機械学習(QML)vs古典機械学習(CML)という構図では、4つの競争軸が存在するだろう:㊀(L2相対誤差が代表的指標である)精度、㊁(適当な学習損失に達するまでのエポック数で計測される)学習速度、㊂(同じ精度を達成するために必要な学習可能パラメータ数で計測される)パラメータ効率、㊃(適当な精度に到達するために必要な)学習データ数。PINNsの文脈で、㊃はピンと来ないかもしれないが、学習データ→コロケーション点と置き換えれば良いだろう。本論文は、㊁と㊂において、量子>古典と主張している。㊀も僅かに、量子>古典である(☞(3)参照)。量子>古典という主張を目指す場合、㊁~㊃をターゲットにすべきと思われる。
ただし、そもそも論的に考えると、本論文のネットワーク・アーキテクチャは、古典ネットワークに量子層を1つ追加しただけである。それだけで、そもそも、そんなに大きな違いが生まれるか?という議論になるだろう。また、量子層を1つ追加しただけで、QPINNsと呼べるのか?という議論もあるだろう。
(1) 一旦「そもそも論=(0)」は扨措き、本論文は、以下のような主張を展開をしている:ある特定のセットアップ(本稿では、便宜上、セットアップ1とした)に対して、PINNsで通常使われる損失関数を使った場合、QPINNsは物理的に意味のない自明解を出力する。そこで、新たな物理制約を課すと、パラメータ効率と精度が向上した(☞精度について(3)参照)。
つまり、無邪気に量子優位性を期待して、PINNs→QPINNsと”量子化”すると、特定のセットアップ(セットアップ1)では、自明解が出力されてしまう。しかし、そこで諦めずに踏ん張って、工夫を凝らすと、PINNsより性能が上がることが(特定のセットアップで)起こる。言葉を替えると、特定のセットアップで、QPINNsは ハイリスク・ハイリターンと解釈することができるだろう。そして、違うセットアップ(セットアップ2)では、切り替えのインセンティブは乏しいと思われる(☞(2)参照)。
(2) 【4】(3)2⃣㈠で記述(既述)した通り、定性的に、セットアップ2の結果は、やや肚落ちしない。エネルギー保存則損失項とは異なる損失項を考慮すれば、肚落ちする結果が得られるだろうか。なお定量的な結果をそのまま飲み込んだ場合でも、精度の文脈でPINNsからQPINNsに替えるインセンティブは、はっきり言ってないだろう。
異なる損失項を考慮すれば・・・と同じ発想で、(古典)PINNsにも何らかの損失項を別途考慮すれば、L2相対誤差が低減するということがあるだろうか。
(3) 本論文には、QPINNsはPINNsと比較して、最大19%高い精度を達成する、と書いてあるが、これは「19%少ない学習可能パラメータ数で、QPINNsはPINNsと同程度の精度を達成する」の誤植であろう。精度(L2相対誤差)は、セットアップ1(真空の場合)で、高々4.3~4.5%である。「高々」と表現したが、精度でQMLがCMLを上回る程度は、この程度の水準が信頼できる。
韓国科学技術院(KAIST)の研究者は、多成分多孔質材料(以下、MVPM)に対して、その基底状態に対応する化学構造を正確に予測・設計する枠組みを開発した、と発表(25年8月22日)[*127]。MVPMは、同一骨格内に複数の異なる化学構成単位(=成分)を有する多孔質材料である。単純多孔質材料と比較して、設計の自由度が高まり、特性・機能の向上が期待できる。その反面、MVPMの設計複雑性は指数関数的であり、基底状態の構成を正確に予測・設計することが大きな課題となっている。ステレオタイプな発想ながら、指数関数的複雑性への対処というお題なので、量子コンピューティングの出番となる。
[*127]は、基底状態を予測するために(NISQでは定番の)VQEアルゴリズム🐾1を採用している。加えて、2つの工夫を凝らした:(1)符号化の工夫、(2)コスト関数の工夫、である。具体的に概略を述べると、(1)は、グラフ・ベースの表現を用いてリンカー🐾2の種類を量子ビットとして符号化する。(2)は、VQEのコスト関数であるハミルトニアンに、"物理的な制約"を直接反映させた。コスト関数に"物理的な制約"を反映させるという発想は、PINNsの発想である。
🐾1 正確にはサンプリングベースのVQE(Variational Quantum Eigensolver)。サンプリングVQEでは、量子回路によって準備された試行状態の測定結果をサンプリングすることによって、エネルギー期待値を評価する。サンプリングとは、量子回路を繰り返し実行して結果を測定するプロセスを指す。[*127]で提案された枠組みは、理論的に、サンプリングVQEと相性が良い。
🐾2 リンカーとは、2つ以上の分子をつなげる化学物質、という理解で良いのだろう。
【2】詳 細
(1) 符号化
符号化の工夫について、少し詳しく述べると、以下の通りである:量子ビットは、サイトとリンカーのペア毎に割り当てられる。量子ビット値0は、サイトにリンカーが存在しないことを意味する。量子ビット値1は、リンカーが存在することを示す。
量子ビット間の相互作用は、G(i,j,wi,j)と表記されるグラフ・ベースのフレームワーク表現によって記述される。添え字iとjは、単位セル内の異なるリンカー・サイトを表し、各順序付きペア(i,j)がエッジを定義する。エッジは、トポロジカル接続🐾3、または空間的隣接性🐾4のいずれかを表し、間接的な相互作用を可能にする。
🐾3 サイトが互いに直接接続されている場合の、エッジの状態を指す。和訳は、直訳なので、味わいはない。
🐾4 サイトは互いに直接接続されていないが、最近傍の次に近く配置されている場合の、エッジの状態を指す。和訳は、直訳なので、味わいはない。
(2) コスト関数
コスト関数の工夫について、もう少し詳しく述べると、以下の通りである:コスト関数(ハミルトニアン)は3項に分解される。比率項、占有項、バランス項の3つである。なお、PINNsで言うところのグローバル重みは、1.0。PINNsで言うところのローカル重みは、1/1。
比率(ratio)項は、異なるリンカーの比率を、設定した比率に強制する(制約する)。占有項は、各リンカー・サイトが、正確に1つのリンカーによって占有されるようにする強制する(制約する)🐾5。バランス項は、幾何学的に最適なリンカー配置を強制する(制約する)🐾6。
なおコスト関数に、リンカー適合性や立体障害🐾7といった化学的制約は考慮されていない(が、今後、考慮されるかもしれない)。
🐾5 この制約(占有項)は、非物理的な化学的構成が解空間に入ることを防ぐ。
🐾6 バランス項には、サイトのペア(i,j)に応じて重みwi,jが考慮される。ここでwi,j=di,jaであり、di,j=ノードiとノードjとの間の距離である。感度パラメータと呼ばれている指数aは、トポロジカル接続(☞🐾3)では1、空間的隣接性(☞🐾4)では0以上1未満の数値である。
🐾7 分子内および分子間で分子を構成する各部分がぶつかることによる回転などの制限のこと。
【3】検証結果
[*127]で提案した枠組み(符号化とコスト関数の工夫)が、実際に機能するかを検証した。IBMのQiskitを使って量子回路を構成している。具体的には、既知の4種類のMVPMに対して、シミュレータ🐾8を使った古典シミュレーションを行った。古典シミュレーションは、量子ノイズ無しである。実機🐾9を使った量子シミュレーションは、計算に必要な量子ビット数が最も少なくて済む、MVPM1種類に対して行った。
(1) 古典シミュレーション
古典シミュレーション結果は、固定シードを使用して、128回の独立したVQEの結果を平均することで導出されている。また、最適化計算における反復回数は300回である。4種類のMVPM全てに対して、(最小エネルギーに対応する)最小ハミルトニアンを出力する確率が、最も高かった。そして、最小ハミルトニアンに対応する化学構造は、実験的に得られている構造と一致した。
(2) 量子シミュレーション
量子シミュレーションでは、量子計算リソースの制約により、最適化計算における反復回数は50回である。[*127]は、量子シミュレーションの結果は、㊀明確な収束傾向を示した、㊁古典シミュレーションの結果と非常に良く一致している、㊂十分な反復回数であれば、最適値に近づくことが期待される、と甘々な評価を下している(☞【4】考察)。
🐾8 IBMのAerシミュレータ。
🐾9 IBMのibm_kyiv。量子ビット数は127。
【4】考 察
【3】(2)の㊀は、agree。㊁は、もやもや。㊂は希望的観測に過ぎず、コメントできない。
㊁については、反復回数20回位までは、良い一致を示しているが、それ以降は差が解離するばかり。もっとも、それは、量子ノイズの蓄積によるもので、逆に当然である、という穿った見方が出来るかもしれない。ただ(、IBMプラットフォームなので何らかの)量子誤り緩和を適用しているはずであり、その効果を示すことで、量子ノイズに対する深い議論ができたはずである。それが示されていないのは、やや残念。
PINNs(Physics-Informedニューラルネットワーク)並びにニューラル演算子は、学習データに依存しているため、 実際のシナリオで適用性が制限されている。このような問題意識の下、英国のリーズ大学及びユニバーシティ・カレッジ・ロンドンの研究者は、「物理法則のみを活用する、教師なし(つまり、学習データ不要である)学習フレームワーク」を提案した論文[*113](以下、本論文)を発表した(2025年2月26日@arXiv)。本論文では、このフレームワークを、PIPNO(Physics-Informed Parallel Neural Operator)と呼んでいる。Parallelとは次の意味である:PIPNOのニューラル演算子部分は、2つのニューラル演算子が並走する、アンサンブル学習を採用している。2つの内の一つは、FNO🐾1と見做すことが可能であり、もう一つはDeepONetの思想を承継している。
なお、本論文は、誤植が多い🐾2。
🐾1 FNO=フーリエ・ニューラル演算子である。
🐾2 例えば(酷いところでは)、楕円型偏微分方程式であるナヴィエ・ストークス方程式が、放物型偏微分方程式と紹介されている。式の間違いも散見される。
【1】本論文の主張
本論文は、以下を主張する:
(1) PIPNOは以下の利点を有する。
㊀ PIPNOは、教師なし学習モデルである。つまり、学習データ(ラベル付きデータ)が不要である。加えて、いかなる仮定や事前知識も必要とせずに、偏微分方程式の解を予測することができる。
㊁ PIPNOはPIFNOに比べて、多くのケースで予測誤差が小さい(☞【4】(4)表)。
(2) PIPNOは、以下のような欠点を有する。
㊀ 非線形が強い物理系の解析では、PIPNOはPIFNOに劣る🐾3(☞【4】(4)表及び【5】(1))。
㊁ 損失関数の最適な重みを決定し、モデルに最適な構成パラメータを設定するための標準化された手順が欠如している。
㊂ 均一グリッド🐾4は、適用範囲を制限する可能性がある。
㊃ 微分における数値離散化🐾5は、固有の誤差をもたらす。
🐾3 具体的に述べると、ナヴィエ・ストークス方程式に対しては、PIPNOはPIFNOより、予測誤差が大きい。
🐾4 PIPNOは、フーリエ空間での演算を含むので、均一グリッドを採用せざるを得ない。
🐾5 PIPNOでは、「非効率な」自動微分は、採用されていない。代わりに、有限差分とフーリエ空間での差分が用いられる。
【2】事前整理
(0) 関数回帰モデリング
学習フレームワークとしてのニューラル演算子の設計とは、積分カーネルの設計である。PIPNOは、この理念の下、積分カーネルを設計している。関数回帰モデリング(本論文では、「関数近似」という文言が使われている)は、学習フレームワークとしてのPIPNOを理解する一助となる。
先述の通りPIPNOのニューラル演算子箇所の半分は、FNOと見做すことが可能である。それは、本論文では、Pnet2と呼ばれている。Pnet1と呼ばれているニューラル演算子は、学習フレームワークとしては「関数回帰モデリング」と見做すことが可能であろう。本論文でもPnet1は、関数近似と学習プロセスが類似している旨の記述がある。
関数回帰モデリングとは、次のような回帰プロセスである:離散点において経時的に観測されたデータを、滑らかな未知関数からサンプリングしたデータとして捉え直し、未知関数をシンボリック回帰の要領で推定するプロセス。具体的には、適当な基底関数の線形結合で、未知関数を表現する。多くの場合、基底関数には、フーリエ級数、多項式関数あるいはスプライン関数が用いられるが、動径基底関数を用いることもできる。[*114]、ではガウス型動径基底関数(の線形結合)を用いた関数回帰モデリングが提案されている。PIPNOでも、ガウス型動径基底関数(の線形結合)を使った関数回帰モデリングが用いられている。
ガウス型動径基底関数(の線形結合)を使った関数回帰モデリングで求めるべきパラメータは、結合係数と、 ガウス型動径基底関数のパラメータである。ガウス型動径基底関数は、RBF(Radius Basis Function)カーネルと呼んだ方が馴染みがあるかもしれない。普通のRBFカーネルは、
RBFカーネル(x)=exp(-x2/2σ2)
である。ガウス型動径基底関数のパラメータとは、上式のσである。多くの場合、最尤法を使って、パラメータを求める。[*114]では、正則化対数尤度関数の最大化によって、パラメータを求めている。つまり、制約条件を課した最適化問題を解いている。PIPNOでは、「物理法則を制約条件として課した最適化問題を、ニューラルネットを使って解く」ことによって、パラメータを求めている(☞【3】(3))。
繰り返しになるがPnet1は、パラメータを求めるアプローチが異なるだけで、本質的には、「関数回帰モデリングと同じ学習フレームワークである見做すことが可能である」と言って良いだろう。もちろん、ディテールは異なる(☞【3】(2))。
(1) ガウス確率場とMatérnカーネル
0⃣ 確率場
ベクトル t = (t1,・・・, tn)を引数に持つ確率変数を、確率場(random field)と呼ぶ[*115]。逆に言うと、確率変数が構成要素であるベクトル空間となるだろう。確率変数が、正規分布(ガウス分布)に従う場合の確率場を、ガウス確率場と呼ぶ。
1⃣ ガウス確率場とガウス過程
応用上は、ガウス確率場とガウス過程とを、本質的に同一視しても、それほど困らない(はず)。しかし、数学的な構成方法は異なるらしく[*116](正確には、そう推量しているだけ)、ガウス確率場とガウス過程とを数学的に同一視することは、難しいらしい。ガウス確率場とは、ガウス過程の特殊なケースである❚補足1❚と書いているサイト[*117]もあるが、それほど単純ではないようである。とは言え、”応用上であれば”、ガウス確率場とガウス過程とを区別する必要性は小さいだろうと結論している。
❚補足1❚ 平均0のガウス確率場は、2点相関関数(共分散関数)という1変数関数で、完全に特徴付けられるという良い性質を持つ。2点相関関数の2点は、2つのベクトルx=(x1,・・・,xm)とx’=(x’1,・・・,x’m)で表すことができる。|x-x’|=rが、1変数である。ここで、ベクトルx及びx’はm次元という一般的な形式にした。サイト[*117]では、2次元の特殊なケースがガウス確率場で、一般のm次元がガウス過程である、と書いている。
2⃣ Matérnカーネル
Matérnクラスのカーネル関数(Matérnカーネル)は、RBFカーネルよりも滑らかでない関数を生成したいときに使われる[*118]。ただし、本論文では全て、Matérnカーネルの「滑らかさを表すパラメータ」νを ν→∞としている。Matérnカーネルでν→∞とした場合は、RBFカーネルに一致するから、RBFカーネルを考えていることになる。
(2) 本論文で扱われる基礎方程式に関する簡単な説明
馴染みが薄い❶圧密方程式、❷アレン・カーン方程式並びに、❻浅水方程式について、簡単な説明をつける。❸マックスウェル方程式、➍シュレーディンガー方程式、❺ナヴィエ・ストークス方程式は割愛。
❶ 圧密方程式
圧密とは、飽和土に外力を作用させたときの、飽和土の変形過程(変形現象)のことである。飽和土とは、(土の)間隙が水で飽和した土のことである。丁寧に説明すると、次のようになる:飽和土からなる供試体or地盤に、外力を作用させると、飽和土の中には、過剰水圧が発生する。このとき、外力作用に遅れて過剰水圧が消散し、その過程で飽和土が水を排出(吸入)しながら、 変形(沈下)する。この変形現象を、圧密と呼ぶ[*119]。
本論文では、テルツァーギ(Terzaghi)の圧密方程式と呼ばれる方程式が、取り上げられている。圧密方程式と言えば、暗黙的にテルツァーギ(Terzaghi)の圧密方程式を指す(らしい)。圧密係数と呼ばれる(圧密方程式に含まれるラプラシアンの前に付く係数)𝐶𝑣は、ダルシーの定数/(水の単位体積重量×体積圧縮係数)で表される。 体積圧縮係数は、ヤング立とポアソン比から計算される。𝐶𝑣は、正である(ため、圧密方程式が「消散過程」を記述することが保証される)。
放物型偏微分方程式であるこの方程式は、土の圧密挙動を記述しており、荷重下における土の変形の時間経過と過剰間隙水圧の「消散過程」を研究するために使用される。また、土質工学における様々な種類のインフラの圧密プロセス・シミュレーション、沈下予測、および沈下制御手順の設計のための理論的根拠を提供する。
❷ アレン・カーン方程式
ざっくり言うと反応拡散方程式であり、PINNsの代表的な適用例として(も)知られている。反応拡散現象を記述する以外に、界面発達(多成分合金/化学反応/結晶成長)、画像セグメンテーション、形状最適化など、様々な問題のモデル化に広く用いられている。放物型偏微分方程式である。
アレン・カーン方程式をフェーズ・フィールド・モデルを記述する(近似する)方程式と見做したとき、
(この方程式に含まれるラプラシアンの前に付く)係数ε2の物理的な意味は、界面の幅である(正確には、εが界面の幅を表す)[*120]。したがって、それなりに小さい値になる(はずである)。なお本論文では、ε2が、εとなっている。
ちなみに、フェーズ・フィールド・モデルは、凝固・結晶成長シミュレーション手法である。同モデルでは、相成長を「フェーズ・フィールド」の時間変化として取り扱う。フェーズ・フィールドとは、液相から固相へに対応して、値が0 から1に変化するスカラー連続関数である。このモデルでは、フェーズ・フィールドの時間変化は、自由エネルギーの変分に比例するという仮定が用いられる。また、このモデルの対象は当初、純金属であったが、2 元系合金、多元系合金、多相系合金へと拡張された[*121]。
❻ 浅水方程式
浅水方程式は、浅水域の流体現象を記述する基礎方程式で、双曲型偏微分方程式である。河川、湖沼、海洋の沿岸域における水の流れのように、流体の深度が水平スケールよりもはるかに小さい状況に適している。そのため、洪水波の予測、潮汐、津波、高潮のシミュレーション、河川洗掘の研究、都市排水システムのシミュレーションなどに広く用いられている。
【3】PIPNOの技術要素
(1) グリーン関数を用いて偏微分方程式を解くアプローチとの類似性
良く知られているように、外力項(あるいは駆動力)fが存在する偏微分方程式N[∂]u(x,t)=f(x,t)の解は、グリーン関数G(x,t;x’,t’)を使って、
u(x,t)=∫∫G(x,t;x’,t’)f(x’,t’)dx’dt’
と表すことができる。なおN[∂]は、偏微分作用素∂/∂t及び∂/∂xの任意多項式である。PIPNOでは、これを拡張変形する。外力項がない偏微分方程式でも扱えるように、fを入力関数a(x,t)に換える。グリーン関数は、積分カーネルκと見做す。
u(x,t)=∫∫κ(x,t;x’,t’)a(t’,x’)dx’dt’ +g(x,t)
g(x,t)という余計な関数が付いてくるが、あまり気にしない(単なる調整役と見る)。
(2) 積分カーネルの設計
ニューラル演算子の要諦は、積分カーネルの設計にあるという理念の下、PIPNO用の積分カーネルを設計する。κは2つに分けられる。こうすることで、「並列演算子学習の相補的な性質により、汎化性能が向上する」と、本論文は主張している。
u(x,t)=∫∫(κ1(x,t;x’,t’)+κ2(x,t;x’,t’))・a(x’,t’)dx’dt’ +g(x,t)
=∫∫κ1a(x’,t’)dx’dt’ +∫∫κ2a(x’,t’)dx’dt’+g(x,t)
=ξ1Pnet1+ξ2Pnet2
そして、∫∫κ1a(x’,t’)dx’dt’を、関数回帰モデリングとして扱う。∫∫κ2a(x’,t’)dx’dt’+g(x,t)は、FNOとして扱われる❚補足2❚。ここで、関数回帰モデリングとの類似性を示す。[*114]の記号・記法を使うと
yα=βα+∫β(t)xα(t)dt+εα
となる。入力は{xα(t)}(α=1,2,・・・,n)で、出力が{yα}(α=1,2,・・・,n)である。xα(t)は、ガウス型動径基底関数の線形結合で表される。出力yαはデータである(PIPNOの場合は、関数である)。
β(t)は、滑らかな関数パラメータである。PIPNOの場合、β(t)が積分カーネルに該当する。関数回帰モデリングにおいて、β(t)もガウス型動径基底関数の線形結合で表される。PIPNOでも同じである。つまり、積分カーネルは、ガウス型動径基底関数(RBFカーネル)の線形結合で表される。Pnet1の積分カーネルは、テイラー・カーネルと呼ばれている🐾6。テイラーはテイラー級数のテイラーであり、積分カーネルが線形結合形式であることから、その名を冠している。また、PIPNOの場合、RBFカーネル及び入力関数a(x,t)は、ガウス確率場(ガウス過程)から自動的に生成される。
なお、ξ1とξ2の比率は、2: 1が推奨されている。
🐾6 Pnet2の積分カーネルは、フーリエ・カーネルと呼ばれている。
❚補足2❚ Pnet2は、やや複雑なプロセスを経る。ここでも、並列学習を行う。具体的には、フーリエ空間での学習と物理空間での学習を並走させ、それぞれの結果を非線形活性化関数GeLUに入力する。このネットワークアーキテクチャは、残差ネットワーク(ResNet)のアイデアを踏襲している。
(3) 損失関数
物理法則を制約条件として課した最適化問題は、損失関数を最小化することで、最適化される。全体の損失関数は、係数1×PDE損失+係数2×境界損失である。係数1及び2は(PINNsの用語では)グローバル重みであり、具体的には「係数1=5、係数2=2」とされている。
【4】比較結果
(1) 計算ワークフロー
0⃣ 為念:計算環境
すべてPytorchで実装され、1次元数値実験はNVIDIA Tesla T4 GPUカードで実行され、2次元数値実験はNVIDIA A100 GPUカードで実行された。
1⃣ ハイパーパラメータ等
オプティマイザー・・・Adam
初期学習率・・・1×10−3
学習率スケジューリング
1次元偏微分方程式の場合、100エポックごとに50%減少(エポック数合計=500)。
2次元偏微分方程式の場合、25エポックごとに50%減少(エポック数合計=200)。
バッチサイズ
1次元・・・20
2次元・・・10
テスト・・・1
2⃣ 学習データに相当する初期入力関数及びグランドトルゥース
初期入力関数a(x,t)は、ガウス確率場を使って、基本的には1,100個生成する。1,000は学習用で、100個はテスト用である。その場合、グランドトルゥースも1,100回実行される。ナヴィエ・ストークス(NS)方程式と浅水方程式では、初期入力関数の生成は、半分の550個で500が学習用、50個がテスト用である。
グランドトルゥースはNS方程式を除いて、「有限差分形式で離散化した支配方程式を、数値積分して解いた数値計算解」である。数値積分手法は、4次のルンゲ・クッタ法である。NS方程式は、スペクトル法(フーリエ・スペクトル法)を用いて解いた数値計算解である。
3⃣ その他
基礎方程式❶と❷には周期境界条件が課される。❸~❻は、周期境界条件ではない、適当な境界条件が課される。Matérnカーネルは、全てのケース(基礎方程式)で、滑らかさを表すパラメータνが∞と指定されるので、実質的にRBFカーネルを指定していることになる。つまり、パラメータ(𝜎, 𝑙, 𝜈)で指定されるMatérnカーネルは、パラメータ(𝜎, 𝑙)で指定されるRBFカーネルであり、具体的には、σ2×exp(-x2/2ℓ2)である(引数をxとしている)。ℓは相関の範囲を制御する長さスケール、σは生成される確率場の振幅である。
(2) 比較の対象となった基礎方程式
6つの基礎方程式を扱った:以下、PIPNO実行における補足事項等を付す。
❶ 圧密方程式
圧密方程式は1次元と2次元のケースで扱われているが、本稿では1次元のみ取り上げた。ニューラル演算子は、演算子𝐺:𝑢0(𝑥) → 𝑢(𝑥,𝑡)を学習することを目指す。𝑢は、間隙水圧である。Gは、与えられた初期関数𝑢0(𝑥)と正解関数𝑢(𝑥,𝑡)との間の写像(関数間の写像)である。添え字0は、初期関数であることを示す(以下、同じ)。
圧密係数𝐶𝑣は、0.01に設定されている🐾7。ガウス確率場(GRF)のパラメータ(𝜎, 𝑙, 𝜈)は、(0.5,0.1, ∞)と設定されている。
🐾7 単位がないことはさて置き、この値の水準感や妥当性が、良く分からない。
❷ アレン・カーン方程式
1次元モデルを扱う。ニューラル演算子は❶と同様、演算子𝐺:𝑢0(𝑥) → 𝑢(𝑥,𝑡)を学習することを目指す。𝑢は、濃度である。アレン・カーン方程式を解く際の課題は、主に非線形反応項、鋭い界面、およびマルチスケール ダイナミクスから生じる。物理的に界面の幅を表すε が非常に小さい場合、界面は非常に薄くなり、解は界面に近接して大きな変化を示し、鋭い界面限界をもたらす。さらに、方程式に固有の非線形反応項 𝑢 −𝑢3は、解の複雑さを高め、数値アルゴリズムの収束を妨げる可能性がある。
εの2乗が、0.0001に設定されている(つまり、界面の幅は0.01)。おそらく、良い塩梅に設定しているのであろう。GRFのパラメータ(𝜎, 𝑙, 𝜈) = (0.4,0.1, ∞)と設定されている。
❸ マックスウェル方程式
均質媒質で満たされた1次元モデルを扱う。ニューラル演算子は、演算子𝐺:𝐸0(𝑥) → [𝐸(𝑥,𝑡), 𝐻(𝑥,𝑡)]を学習することを目指す。Eは電場でHは磁場である。
マクスウェル方程式を解くことの難しさは、「マクスウェル方程式が、マルチスケール特性を持つ電場と磁場の時空間相互作用を伴う、ベクトル偏微分方程式の高度に結合したシステム」であることに起因する。方程式の解は、特に電磁場の伝播や振動現象を記述する場合に、通常、顕著な高周波特性を示す傾向がある。
物理的な設定は、誘電率=1、透磁率=1、電荷密度=0、電流密度= 0である。違和感は全くない。GRFのパラメータ(𝜎, 𝑙, 𝜈) = (0.1,0.1, ∞)と設定されている。
➍ シュレーディンガー方程式
1次元モデルを扱う。ニューラル演算子は、演算子𝐺: 𝜓0(𝑥) → [𝑢(𝑥,𝑡), 𝑣(𝑥,𝑡)] = 𝜓(𝑥,𝑡) を学習することを目指す。ここで、𝜓(𝑥,𝑡)は波動関数である。𝑢(𝑥,𝑡)は𝜓(𝑥,𝑡)の実部で、𝑣(𝑥,𝑡) は𝜓(𝑥,𝑡)の虚部である。
時間依存シュレーディンガー方程式を解くことの難しさは、主にその高度な非線形性と強く結合した特性に起因しており、特に高次元空間や多粒子系では、波動関数の複雑さによって計算リソースが非常に要求される。波動関数は、高周波振動を特徴とする場合があり、これは提示された結果にも反映されている。時間発展過程は精度と安定性の両方を満たす必要があり、時間依存または非滑らかな条件を持つポテンシャルは、数値解の難易度を高める。
量子状態の微細な特徴を捉えるには高解像度グリッドと精密な時間ステップも必要であり、計算負荷がさらに増加する可能性がある。さらに、数値実験から、初期条件の選択が精度と結果に大きな影響を与える可能性があることも判明しており、非滑らかな変動初期条件は高周波振動特性を生み出す傾向が強い。
物理的な設定は、プランク定数ℏ=1、ハミルトニアンに現れる質量m=1である。違和感はない。GRFのパラメータ(𝜎,𝑙, 𝜈) = (0.5,0.4, ∞)と設定されている。
❺ ナヴィエ・ストークス(NS)方程式
2次元モデルを扱う。ただし、NS方程式は、渦度方程式の変換されている。つまり、変数は速度uから渦度𝜔に変換されている(∇×速度=渦度)。ニューラル演算子は、演算子𝐺:𝜔0(𝑥,𝑦) →𝜔(𝑥,𝑦,𝑡)を学習することを目指す。NS方程式を解くことの難しさは、強い非線形性にある。
物理的な設定は、動粘性係数=0.05であるが、単位がないし、違和感がある。おそらく物理的なイメージなしに設定されているのだろう。しかし、他ケースと異なり、物理的な実体をもたせないと、物理的に意味のないシミュレーションをしていることになりかねないと思われる。また、レイノルズ数の指定がないため、その意味でも、意味がないと思われる。GRFのパラメータ(𝜎,𝑙, 𝜈) = (0.6,0.2, ∞)と設定されている。
❻ 浅水方程式
2次元モデルを扱う。ニューラル演算子は、演算子𝐺:𝜂0(𝑥, 𝑦) → [𝜂(𝑥, 𝑦,𝑡), 𝑢(𝑥, 𝑦,𝑡), 𝑣(𝑥, 𝑦,𝑡)]。ここで、𝜂は水位、𝑢及び𝑣は流速である。浅水方程式を解くことの難しさは、単一の初期関数から、3つの相互に関連する関数の写像を導出することに起因する。
物理的な設定は、水の動粘性係数= 0.002とされているが、これも単位がない。なお、❺の動粘性係数は❻で設定される水の動粘性係数の25倍である。大気圧下における空気の動粘性係数は、水のおよそ15倍である🐾8。600hPaだと25倍くらいになる。GRFのパラメータ(𝜎,𝑙,𝜈) = (0.2,0.1,∞)と設定されている。
🐾8 つまり、動粘性係数は、「動かされ易さ」を体現する指標である。
(3) 比較指標及び比較対象モデル
比較指標は、相対L2誤差、平均絶対誤差(MAE)並びに二乗平均平方根誤差(RMSE)であるが、数値で示されているのは相対L2誤差のみである。
比較対象モデルはPIFNO、つまり、Physics-Informedフーリエ・ニューラル演算子である。本論文は、その理由を、「PIFNOは、現在偏微分方程式を解くのに、強力かつ効果的であることが広く実証されている最先端の方法であるため」と述べている。PIPNOは、PIFNOの改良バージョンと捉えることもできるから、ベンチマークとしては妥当な選択であろう。
(4) 結果
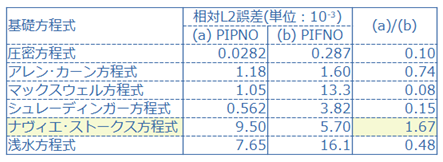
PIPNOとPIFNOを比較した結果を、下表に示す。相対L2誤差の単位が、10-3であることに注意。その理由は、PINNsにおける相対L2誤差のスイート・スポットが、10-3であるからである。相対L2誤差は、対象とする基礎方程式に依存して変化するし、その他条件にも依存するから、この値は粗っぽい推定ではあるものの、目安としては悪くないと考えている。
結果として特筆すべきは、「NS方程式のみ、PIFNOの相対L2誤差が小さい」ことである。その理由の考察は【5】(1)を参照。
※ 下表の最右列(a)/(b)は、本論文中には無い。また(a)/(b)という量に、意味はない。比較のため、便宜上、付加したに過ぎない。
【5】考察
(1) NS方程式のみ、PIFNOの相対L2誤差はPIPNOより小さい。この理由を、本論文は、「グランドトルゥースは、スペクトル法を使用している。PIFNOの原理はスペクトル法に完全に適合している。この一貫性により、PIFNOによる結果とグランドトルゥースとの適合度が向上した」と説明している。つまり、スペクトル法以外の手法で求めた数値解をグランドトルゥースとした場合は、PIPNOが勝てると言っている。本当だろうか?
(2) 全ての基礎方程式に対して、グローバル重みを「PDE損失で5、境界損失で2」というのは無理があるように思える。少なくとも、NS方程式に対しては(レイノルズ数にも依存するが)、PDE損失の重みを境界損失の重みより小さくするのがセオリーであろう。むしろ(5,2)➡(1,10)🐾9くらいではないだろうか。
🐾9 あくまで割合として、(1,10)と書いている。実際に設定する重みとしては、例えば、(0.1,1.0)となるだろう。
(3) 相対L2誤差に関しては、PINNsもPIPNOも大差はない。PIPNOの利点は、やはり「学習データが不要であることに加えて、いかなる仮定や事前知識も必要とせずに、偏微分方程式の解を予測することができる」ということになるのだろう。
【尾注】
(*40 Sifan Wang et al.、AN EXPERT’S GUIDE TO TRAINING PHYSICS-INFORMED NEURAL NETWORKS、https://arxiv.org/pdf/2308.08468.pdf)
(*74 Zhongkai Hao et al.、PINNACLE: A COMPREHENSIVE BENCHMARK OF PHYSICS-INFORMED NEURAL NETWORKS FOR SOLVING PDES、https://arxiv.org/pdf/2306.08827.pdf)
*85 Jacob Varey et al.、Physics-Informed Neural Networks for Satellite State Estimation、https://arxiv.org/pdf/2403.19736.pdf
*86 超伝導方式の量子コンピュータを開発しているフィンランドのスタートアップ「IQM quantum Computers」は、アールト大学とVTT(フィンランド国立技術研究センター)のスピンアウト・スタートアップである。
*87 Katsiaryna Haitsiukevich & Alexander Ilin、IMPROVED TRAINING OF PHYSICS-INFORMED NEURAL NETWORKS WITH MODEL ENSEMBLES、https://arxiv.org/pdf/2204.05108.pdf
*88 Jose Florido et al.、Investigating Guiding Information for Adaptive Collocation Point Sampling in PINNs、https://arxiv.org/pdf/2404.12282)
*89 Ariel Norambuena et al.、Physics-informed neural networks for quantum control、https://arxiv.org/pdf/2206.06287
*90 大塚智之、最適制御の考え方と最近の展開、2016年7月4日、https://www.usss.kyoto-u.ac.jp/wp-content/uploads/2021/03/20160704_Ohtsuka.pdf
*91 孤立スペクトルを持つ系は完全制御可能であるという結果から、導かれる。出所:高見利也・藤崎弘士・宮寺隆之、粗視化描像における量子カオス制御、https://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/1369-3.pdf
*92 https://www.nii.ac.jp/news/release/2021/1104.html
*93 Zhen Zhang et al.、Discovering a reaction-diffusion model for Alzheimer’s disease by
combining PINNs with symbolic regression、https://arxiv.org/pdf/2307.08107
*94 厚生労働科学研究費補助金(認知症対策総合研究事業)総合研究報告書「都市部における認知症有病率と認知症の生活機能障害への対応、H24総合報告書_Part3(http://www.tsukuba-psychiatry.com/wp-content/uploads/2013/06/H24Report_Part3.pdf)の図9。
*95 厚生労働省老健局、認知症施策の総合的な推進について(参考資料)、令和元年6月20日、https://www.mhlw.go.jp/content/12300000/000519620.pdf
*96 https://www.tmghig.jp/research/topics/201703-3382/
*97 https://www.mhlw.go.jp/houdou/2009/03/h0319-2.html ただし、こちらはさらにデータが古く、発表が平成21年、調査は平成18年度~20年度である。
*98 岩坪威、ヒト脳疾患画像データベース統合化研究、https://biosciencedbc.jp/gadget/rdprog_over/iwatsubo.pdf
*99 荒井 啓行、アルツハイマー病の発症前診断と MCI、https://www.jstage.jst.go.jp/article/clinicalneurol/49/11/49_11_838/_pdf
*100 F. O. de Franca et al.、Interpretable Symbolic Regression for Data Science:Analysis of the 2022 Competition、https://arxiv.org/pdf/2304.01117
*101 https://www.science.org/content/article/researchers-plan-retract-landmark-alzheimers-paper-containing-doctored-images
・・・
*109 Jaemin Seo、Solving real-world optimization tasks using physics-informed neural computing、https://www.nature.com/articles/s41598-023-49977-3
・・・
*113 Biao Yuan et al.、High-fidelity Multiphysics Modelling for Rapid Predictions Using
Physics-informed Parallel Neural Operator、https://arxiv.org/pdf/2502.19543
*114 荒木由布子・小西貞則、動径基底関数展開に基づく関数回帰モデリング、応用統計学VoL.33, No.3(2004),pp.243-256、https://www.jstage.jst.go.jp/article/jappstat1971/33/3/33_3_243/_pdf
*115 栗木哲、特集/統計的思考法のすすめ|確率場の幾何 統計的発見のための積分幾何学、数理科学 NO. 687, SEPTEMBER 2020、pp.1-7、https://www.ism.ac.jp/~kuriki/paper/suurikagaku-fin.pdf
*116 飛田武幸、Gauss型確率場の変分(ガウス型確率場:確率変分解析及び関連する話題)、https://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/0672-01.pdf
及び、野田明男、Gauss確率場のwhite noise表現(ガウス型確率場 : 確率変分解析及び関連する話題)、https://www.kurims.kyoto-u.ac.jp/~kyodo/kokyuroku/contents/pdf/0672-03.pdf
*117 https://qiita.com/ynakayama/items/dc54c48b94db7bc8d939
*118 https://gochikika.ntt.com/Modeling/gp_regression.html
*119 野田利弘、地盤工学会中部支部 初級集中講座 圧密、平成22年7月10日、https://jgs-chubu.org/wp-content/uploads/pdfupload/download/seminar/pdf/20100710/Noda.pdf
*120 劔持智哉、Allen‐Cahn方程式の数値解に対する漸近的な誤差解析、京都大学数理解析研究所講究録 第2094巻 2018年 pp.82-89、https://core.ac.uk/download/pdf/326051893.pdf
*121 鈴木俊夫他、フェーズフィールドモデル、日本マイクログラビティ応用学会誌 Vol. 19 No. 1 2002 (pp.2-8)、https://www.jstage.jst.go.jp/article/jasma/19/1/19_2/_pdf
*122 Wei Zhoua and Y.F. Xua、Data-Guided Physics-Informed Neural Networks for Solving Inverse Problems in Partial Differential Equations、https://arxiv.org/pdf/2407.10836
*123 Ziv Chen et al.、Quantum Physics-Informed Neural Networks for Maxwell’s Equations: Circuit Design, “Black Hole” Barren Plateaus Mitigation, and GPU Acceleration、https://arxiv.org/pdf/2506.23246
・・・
*126 K. Ishitsuka et al.、Reliable and Practical Inverse Modeling of Natural-State Geothermal Systems Using Physics-Informed Neural Networks: Three-Dimensional Model Construction and Assimilation With Magnetotelluric Data、https://agupubs.onlinelibrary.wiley.com/doi/epdf/10.1029/2025JH000683

